單晶銅塑性變形的二維離散位錯動力學模擬研究

王春暉; 孫朝陽; 郭祥如; 魏云燦; 蔡旺

doi:10.13374/j.issn2095-9389.2021.04.21.005

單晶銅塑性變形的二維離散位錯動力學模擬研究

doi: 10.13374/j.issn2095-9389.2021.04.21.005

王春暉^{1, 2},
孫朝陽^{1, 2, 3, ,},
郭祥如⁴,
魏云燦^{1, 2},
蔡旺^{1, 2}

1.
北京科技大學機械工程學院, 北京 100083
2.
北京科技大學金屬輕量化成形制造北京市重點實驗室, 北京 100083
3.
北京科技大學順德研究生院, 佛山 528000
4.
天津理工大學天津市先進機電系統設計與智能控制重點實驗室, 天津 300384

基金項目: 國家自然科學基金委員會與英國皇家學會合作交流資助項目（51911530209）；國家自然科學基金面上資助項目（52175285）；國家自然科學基金NSAF聯合資助項目（U1730121）；北京科技大學順德研究生院科技創新專項基金資助項目（BK19CE008）

詳細信息

通訊作者:
E-mail: suncy@ustb.edu.cn

中圖分類號: TG142.71
計量
- 文章訪問數: 853
- HTML全文瀏覽量: 350
- PDF下載量: 58
- 被引次數: 0
出版歷程
- 收稿日期: 2021-04-21
- 網絡出版日期: 2021-09-24
- 刊出日期: 2021-10-12

Investigation of the plastic deformation of single crystal copper using a two-dimensional discrete dislocation dynamics model

WANG Chun-hui^{1, 2},
SUN Chao-yang^{1, 2, 3
, ,},
GUO Xiang-ru⁴,
WEI Yun-can^{1, 2},
CAI Wang^{1, 2}

1.
School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China
2.
Beijing Key Laboratory of Lightweight Metal Forming, University of Science and Technology Beijing, Beijing 100083, China
3.
Shunde Graduate School, University of Science and Technology Beijing, Foshan 528000, China
4.
Tianjin Key Laboratory for Advanced Mechatronic System Design and Intelligent Control, School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384, China

More Information

Corresponding author: E-mail: suncy@ustb.edu.cn

摘要

摘要: 針對亞微米尺度晶體元器件在加工和服役中出現的反常力學行為和動態變形等問題，基于離散位錯動力學理論建立了單晶銅塑性變形過程的二維離散位錯動力學模型。該模型考慮外加載荷、位錯間相互力和自由表面鏡像力對位錯的作用機制，引入了截斷位錯速度準則。與微壓縮實驗對比驗證了模型的正確性，并且能夠描述力加載描述的位錯雪崩現象。應用該模型分析了不同加載方式和應變率下位錯演化及力學行為，結果表明：當外部約束為力加載和位移加載時，應力應變曲線分別呈現出臺階狀的應變突增和鋸齒狀的應力陡降，位錯雪崩效應的內在機制則分別歸結為位錯速度的隨機性和位錯源開動的間歇性；應變率在10²～4×10⁴ s^?1范圍內，單晶銅屈服應力的應變率敏感性發生改變，位錯演化特征由單滑移轉變為多滑移面激活的均勻變形，位錯增殖逐漸代替位錯源激活作為流動應力的主導機制。
- 單晶銅 /
- 離散位錯動力學 /
- 加載方式 /
- 應變率 /
- 力學行為
Abstract: Microelectromechanical systems (MEMS) that feature components with the same geometrical size as that of an individual grain have been widely used in a variety of industries, including electronics, machinery, energy, transportation, aerospace, and architecture. Owing to the widespread engineering application of MEMS and nanoelectromechanical system devices, including sensors and actuators, submicron scale crystal materials exhibit mechanical behaviors different from those of macroscale materials, such as size effect, intermittent plastic flow, and strain rate effect, that have become significant topics in mechanics and materials research in recent years. Since dislocations are the carriers of plastic deformation, understanding the dislocation mechanism of submicron crystalline materials is crucial for designing and predicting microdevice reliability. To improve the understanding of abnormal mechanical behavior and dynamic deformation of submicron scale crystal components in processing and application, a two-dimensional discrete dislocation dynamics model of single crystal copper for plastic deformation was established based on the discrete dislocation dynamics theory. The effects of applied load, dislocation interactions, and image force by the free surface on dislocations were all considered in the numerical model, and the cutoff weighted dislocation velocity was also introduced. The model can be used to describe the “dislocation avalanche” effect under stress-controlled modes and interpret the dislocation evolution and mechanical behavior under different loading modes and strain rates, as demonstrated by microcompression experiments. When the external loading modes are force control and displacement control, the stress–strain curves show a step-like character under strain and a sharply serrated character under stress, respectively. The randomization of the dislocation velocity and intermittent activation of dislocation sources are the internal mechanisms of the dislocation avalanche effect. The strain rate sensitivity of the yield stress for single crystal copper changes in the strain rate range of 10²–4 × 10⁴ s^?1. The evolution characteristics of the dislocations change from single slip plane to uniform deformations induced by multiple slip planes activation, and the dominant mechanism for the strain rate effect of yield stress is dislocation multiplication rather than dislocation source activation.
- single crystal copper /
- discrete dislocation dynamics /
- loading modes /
- strain rates /
- mechanical behavior

HTML全文

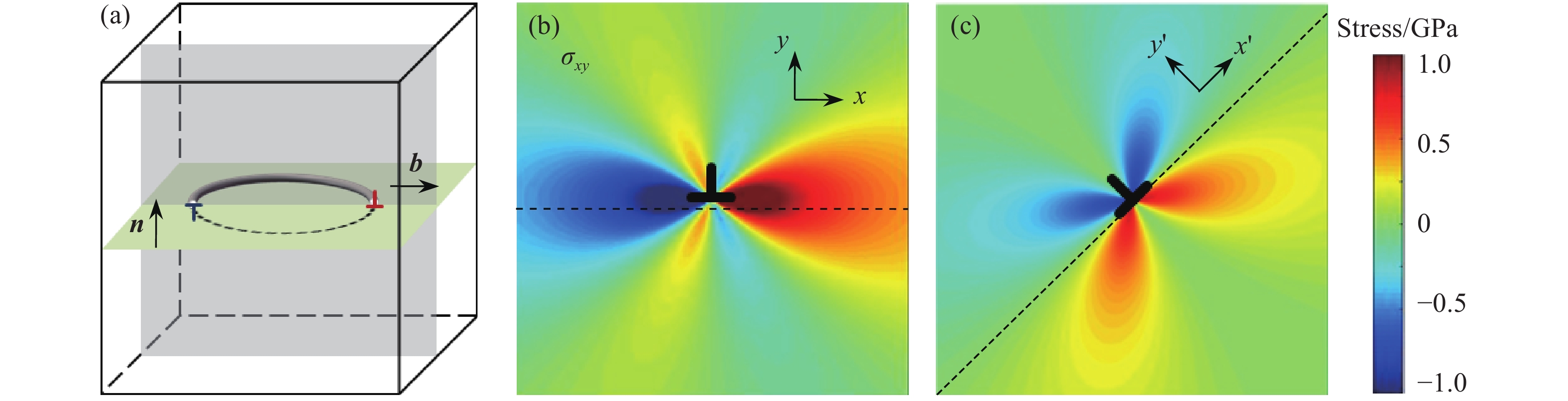
圖 1 位錯的二維簡化及其應力場。（a）位錯線在二維平面的投影示意圖；（b）水平方向和（c）傾斜45°方向正刃型位錯剪切應力場

Figure 1. Two dimensional simplification of and stress field of dislocation: (a) planar representation of the dislocation line on a 2D plane; stress field (σ_xy) around a positive edge dislocation in the (b) horizontal direction and (c) tilt direction with an angle of 45°

下載: 全尺寸圖片幻燈片

圖 2 2D?DDD模型的模擬流程

Figure 2. Flow chart of the 2D?DDD model

下載: 全尺寸圖片幻燈片

圖 3 單晶銅晶體學取向及計算模型。（a）FCC晶體滑移系取向；（b）壓縮載荷下2D-DDD計算模型

Figure 3. Crystallographic orientation and calculation model of single crystal copper: (a) slip system orientation for the FCC crystal; (b) the 2D?DDD model under compression

下載: 全尺寸圖片幻燈片

圖 4 不同加載方式下2D?DDD和3D?DDD計算^[16]及實驗^[36]獲得的單晶銅應力?應變曲線

Figure 4. Stress–strain curves for the 2D?DDD model of the single crystal copper compared with those for the 3D?DDD model^[16] and experiments^[36] at different loading modes

下載: 全尺寸圖片幻燈片

圖 5 不同加載方式下發生一次位錯爆發的應力–應變曲線

Figure 5. Stress–strain curves of dislocation avalanches under different loading modes

下載: 全尺寸圖片幻燈片

圖 6 （a）力控制加載下應力和加權位錯速度隨應變演化；（b）位移控制加載下應力和應變率隨應變演化

Figure 6. (a) Evolution of stress and weighted dislocation velocity with strain under stress-controlled mode and (b) evolution of stress and strain rate with strain under strain-controlled mode

下載: 全尺寸圖片幻燈片

圖 7 不同應變率下的（a）應力?應變曲線；（b）屈服應力；（c）位錯密度?應變曲線；（d）組成應力

Figure 7. Effect of strain rate on the evolution of：(a) stress vs strain; (b) yield stress; (c) dislocation density vs strain; (d) stress composition

下載: 全尺寸圖片幻燈片

圖 8 不同應變率下塑性滑移量分布。（a）10² s^?1；（b）10³ s^?1；（c）10⁴ s^?1；（d）4×10⁴ s^?1

Figure 8. Plastic slip distribution resulting from the strain rates at: (a) 10² s^?1; (b) 10³ s^?1; (c) 10⁴ s^?1; (d) 4×10⁴ s^?1

下載: 全尺寸圖片幻燈片

表 1 單晶銅2D?DDD模擬參數

Table 1. Model parameters used in the 2D?DDD model for single crystal copper

G/GPa	ν	b/nm	ρ_s/m^?2	$l_0^{\rm{ave}} $/nm
42	0.34	0.256	50×10¹²	500

Δl₀/nm	η₁	η₂/(Pa·s)	B₀/(Pa·s)	v_s/(m·s^?1)
50	1.5	9B	10^?4	2.92×10³
Note: G—Shear modulus; v—Poisson’s ratio; b—Burgers vector；ρ_s—Source density; $l_0^{\rm{ave}} $—Mean value of initial length of dislocation source; Δl₀—Standard deviation of initial length of dislocation source; η₁—Enhancement factor; η₂—Correlation coefficient; B₀—Static viscous drag coefficient; v_s—Speed of shear wave.

下載: 導出CSV

259luxu-164

參考文獻(40)

[1]	Liu B, Xu Z W, Li R, et al. In-situ experiment on critical thickness of brittle-ductile transition of single-crystal silicon. Chin J Eng, 2019, 41(3): 343 劉冰, 徐宗偉, 李蕊, 等. 單晶硅脆塑轉變臨界厚度的原位實驗. 工程科學學報, 2019, 41(3):343
[2]	Shui L, Hu Z Q. Creep fracture of a nickel base single crystal superalloy along [011] orientation. Chin J Eng, 2015, 37(5): 615 水麗, 胡壯麒. 一種[011]取向鎳基單晶合金的蠕變斷裂. 工程科學學報, 2015, 37(5):615
[3]	Bai Q S, Hu C, Bai J X, et al. Tensile properties of monocrystalline copper component based on discrete dislocation dynamics. J Plast Eng, 2018, 25(5): 270 白清順, 胡超, 白錦軒, 等. 基于離散位錯動力學的單晶銅構件拉伸特性研究. 塑性工程學報, 2018, 25(5):270
[4]	Dong X H, Wang Q, Zhang H M, et al. Research progress of size effect in microforming. Sci Sinica Technol, 2013, 43(2): 115 doi: 10.1360/ze2013-43-2-115 董湘懷, 王倩, 章海明, 等. 微成形中尺寸效應研究的進展. 中國科學:技術科學, 2013, 43(2):115 doi: 10.1360/ze2013-43-2-115
[5]	Huang G J, Duan Z P, Wang W B. Dynamical analysis on the formation of dislocation pattern in the easy slip stage of single crystals 1. Acta Mech Sinica, 1998, 30(1): 65 黃國君, 段祝平, 王文標. 單晶易滑移階段位錯結構形成的動力學分析. 力學學報, 1998, 30(1):65
[6]	Zhang X, Aifantis K E. Accounting for grain boundary thickness in the sub-micron and nano scales. Rev Adv Mater Sci, 2010, 26(1): 74
[7]	Zhang X, Aifantis K E. Interpreting strain bursts and size effects in micropillars using gradient plasticity. Mater Sci Eng:A, 2011, 528(15): 5036 doi: 10.1016/j.msea.2011.02.049
[8]	Fan H D, Wang Q Y, El-Awady J A, et al. Strain rate dependency of dislocation plasticity. Nat Commun, 2021, 12: 1845 doi: 10.1038/s41467-021-21939-1
[9]	He S L, Jiang W T, Bai J S, et al. Study of dynamical mechanical properties and dislocation dynamics of copper single crystals by discrete dislocation dynamics simulation. IOP Conf Ser:Mater Sci Eng, 2020, 770: 012094 doi: 10.1088/1757-899X/770/1/012094
[10]	Cui Y N. The Investigation of Plastic Behavior by Discrete Dislocation Dynamics for Single Crystal Pillar at Submicron Scale [Dissertation]. Beijing: Tsinghua University, 2014 崔一南. 亞微米單晶柱塑性行為的離散位錯研究[學位論文]. 北京: 清華大學, 2014
[11]	Gao Y. Discrete Dislocation Mechanism on Submicro-Crystal Plasticity [Dissertation]. Beijing: Tsinghua University, 2011 高原. 亞微米晶體塑性的離散位錯機理[學位論文]. 北京: 清華大學, 2011
[12]	Papanikolaou S, Dimiduk D M, Choi W, et al. Quasi-periodic events in crystal plasticity and the self-organized avalanche oscillator. Nature, 2012, 490(7421): 517 doi: 10.1038/nature11568
[13]	Maa? R, Derlet P M, Greer J R. Independence of slip velocities on applied stress in small crystals. Small, 2015, 11(3): 341 doi: 10.1002/smll.201400849
[14]	Csikor F F, Motz C, Weygand D, et al. Dislocation avalanches, strain bursts, and the problem of plastic forming at the micrometer scale. Science, 2007, 318(5848): 251 doi: 10.1126/science.1143719
[15]	Cui Y N, Po G, Ghoniem N. Controlling strain bursts and avalanches at the nano- to micrometer scale. Phys Rev Lett, 2016, 117(15): 155502 doi: 10.1103/PhysRevLett.117.155502
[16]	Cui Y N, Po G, Ghoniem N. Influence of loading control on strain bursts and dislocation avalanches at the nanometer and micrometer scale. Phys Rev B, 2017, 95(6): 064103 doi: 10.1103/PhysRevB.95.064103
[17]	Meyers M A, Gregori F, Kad B K, et al. Laser-induced shock compression of monocrystalline copper: Characterization and analysis. Acta Mater, 2003, 51(5): 1211 doi: 10.1016/S1359-6454(02)00420-2
[18]	Hu J Q, Liu Z L, Erik V D G, et al. Strain rate effects on the plastic flow in submicron copper Pillars: Considering the influence of sample size and dislocation nucleation. Extreme Mech Lett, 2017, 17: 33 doi: 10.1016/j.eml.2017.09.011
[19]	Jennings A T, Li J, Greer J R. Emergence of strain-rate sensitivity in Cu nanopillars: Transition from dislocation multiplication to dislocation nucleation. Acta Mater, 2011, 59(14): 5627 doi: 10.1016/j.actamat.2011.05.038
[20]	Zheng Z B, Balint D S, Dunne F P E. Rate sensitivity in discrete dislocation plasticity in hexagonal close-packed crystals. Acta Mater, 2016, 107: 17 doi: 10.1016/j.actamat.2016.01.035
[21]	Guo X R, Sun C Y, Wang C H, et al. Investigation of strain rate effect by three-dimensional discrete dislocation dynamics for fcc single crystal during compression process. Acta Metall Sin, 2018, 54(9): 1322 doi: 10.11900/0412.1961.2017.00553 郭祥如, 孫朝陽, 王春暉, 等. 基于三維離散位錯動力學的fcc結構單晶壓縮應變率效應研究. 金屬學報, 2018, 54(9):1322 doi: 10.11900/0412.1961.2017.00553
[22]	Agnihotri P K, Erik V D G. On the rate sensitivity in discrete dislocation plasticity. Mech Mater, 2015, 90: 37 doi: 10.1016/j.mechmat.2015.01.009
[23]	LeSar R. Simulations of dislocation structure and response. Annu Rev Condens Matter Phys, 2014, 5(1): 375 doi: 10.1146/annurev-conmatphys-031113-133858
[24]	Anderson P M, Hirth J P, Lothe J. Theory of dislocations. 3rd Ed. Cambridge: Cambridge University Press, 2017
[25]	Van der Giessen E, Needleman A. Discrete dislocation plasticity: A simple planar model. Modelling Simul Mater Sci Eng, 1995, 3(5): 689 doi: 10.1088/0965-0393/3/5/008
[26]	Zheng Z B. Investigation of Cold Dwell Facet Fatigue in Titanium Alloys Utilising Crystal Plasticity and Discrete Dislocation Plasticity Modelling Techniques [Dissertation]. London: Imperial College London, 2016
[27]	Argon A. Strengthening Mechanisms in Crystal Plasticity. Oxford: Oxford University Press, 2007
[28]	Gillis P P, Gilman J J, Taylor J W. Stress dependences of dislocation velocities. Philos Mag:A J Theor Exp Appl Phys, 1969, 20(164): 279
[29]	Benzerga A A. An analysis of exhaustion hardening in micron-scale plasticity. Int J Plast, 2008, 24(7): 1128 doi: 10.1016/j.ijplas.2007.08.010
[30]	Cleveringa H H M, Van der Giessen E, Needleman A. A discrete dislocation analysis of bending. Int J Plast, 1999, 15(8): 837 doi: 10.1016/S0749-6419(99)00013-3
[31]	Fan H D, Li Z H, Huang M S, et al. Thickness effects in polycrystalline thin films: Surface constraint versus interior constraint. Int J Solids Struct, 2011, 48(11-12): 1754 doi: 10.1016/j.ijsolstr.2011.02.026
[32]	Deshpande V S, Needleman A, Van der Giessen E. Plasticity size effects in tension and compression of single crystals. J Mech Phys Solids, 2005, 53(12): 2661 doi: 10.1016/j.jmps.2005.07.005
[33]	Rao S I, Dimiduk D M, Parthasarathy T A, et al. Athermal mechanisms of size-dependent crystal flow gleaned from three-dimensional discrete dislocation simulations. Acta Mater, 2008, 56(13): 3245 doi: 10.1016/j.actamat.2008.03.011
[34]	Uchic M D, Dimiduk D M, Florando J N, et al. Sample dimensions influence strength and crystal plasticity. Science, 2004, 305(5686): 986 doi: 10.1126/science.1098993
[35]	Liang Z Y, Huang M X. Deformation twinning in small-sized face-centred cubic single crystals: Experiments and modelling. J Mech Phys Solids, 2015, 85: 128 doi: 10.1016/j.jmps.2015.09.004
[36]	Zhang J Y, Liu G, Sun J. Strain rate effects on the mechanical response in multi- and single-crystalline Cu micropillars: Grain boundary effects. Int J Plast, 2013, 50: 1 doi: 10.1016/j.ijplas.2013.03.009
[37]	Liang Z Y, Wang X, Huang W, et al. Strain rate sensitivity and evolution of dislocations and twins in a twinning-induced plasticity steel. Acta Mater, 2015, 88: 170 doi: 10.1016/j.actamat.2015.01.013
[38]	Liu Z L, You X C, Zhuang Z. A mesoscale investigation of strain rate effect on dynamic deformation of single-crystal copper. Int J Solids Struct, 2008, 45(13): 3674 doi: 10.1016/j.ijsolstr.2007.08.032
[39]	Guo X R, Sun C Y, Li R, et al. A dislocation density based model for twinning induced softening of TWIP steel. Comput Mater Sci, 2017, 139: 8 doi: 10.1016/j.commatsci.2017.07.013
[40]	Wang C H, Sun C Y, Qian L Y, et al. Dynamic mechanical behaviour induced by adiabatic temperature rise of Fe?Mn?Al?C steel. Mater Sci Technol, 2021, 37(3): 280 doi: 10.1080/02670836.2021.1885580