Prediction model for the migration trajectory and velocity of ore-rock dispersions in an orepass storage section
-
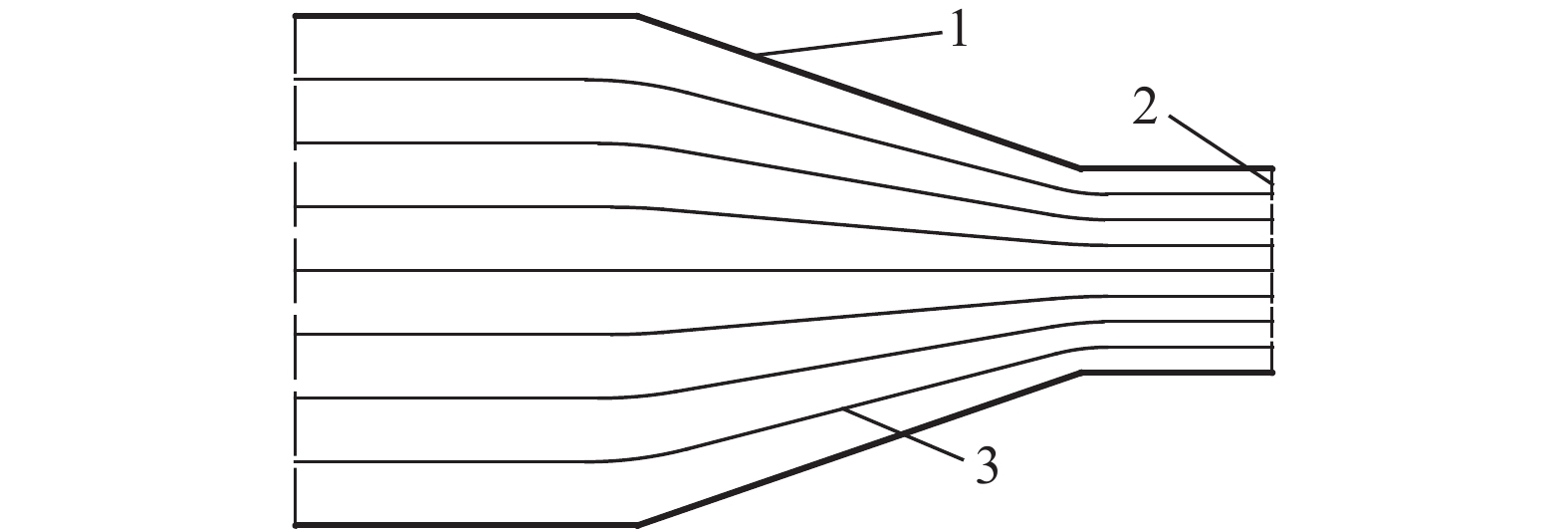
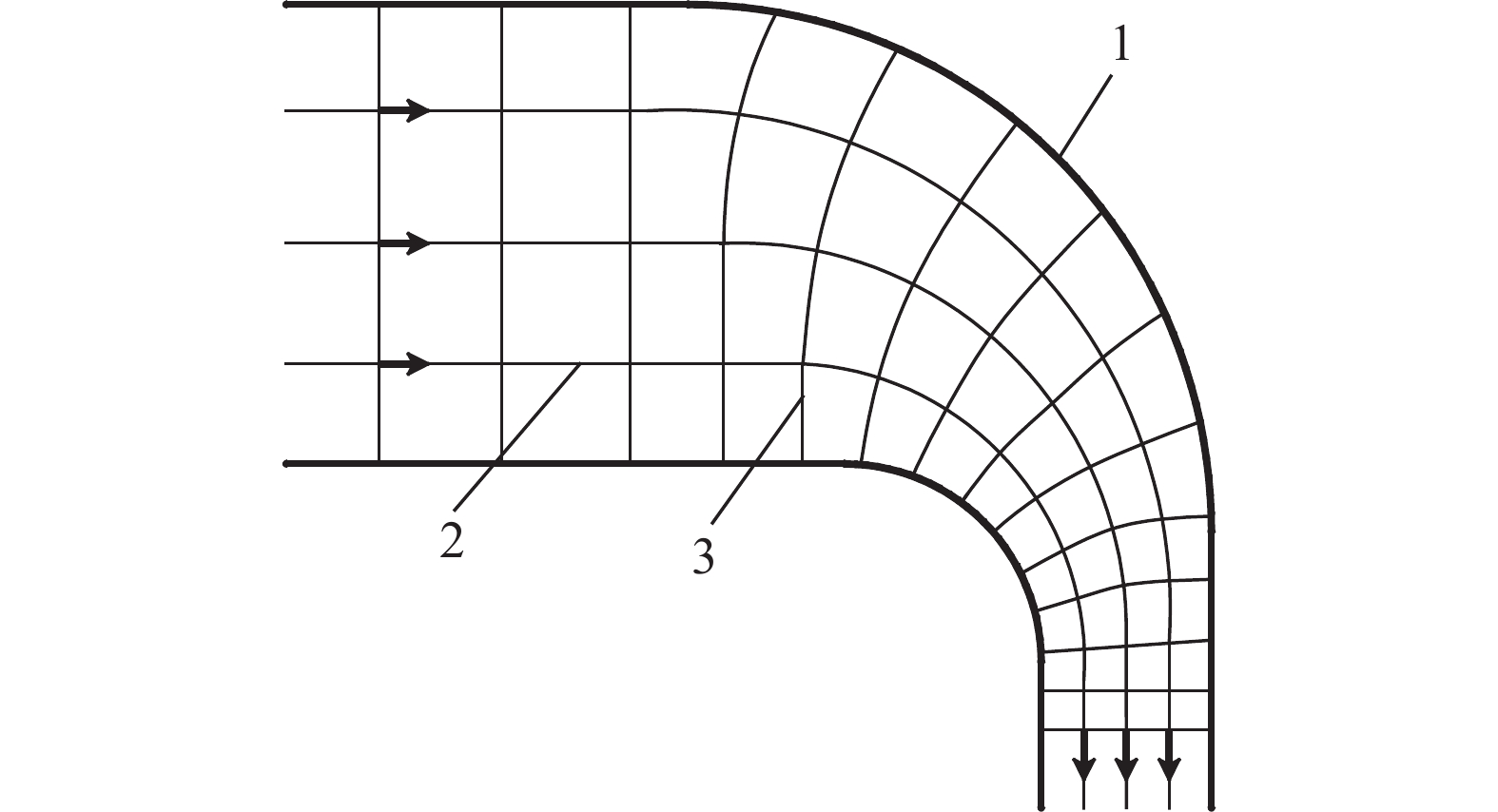
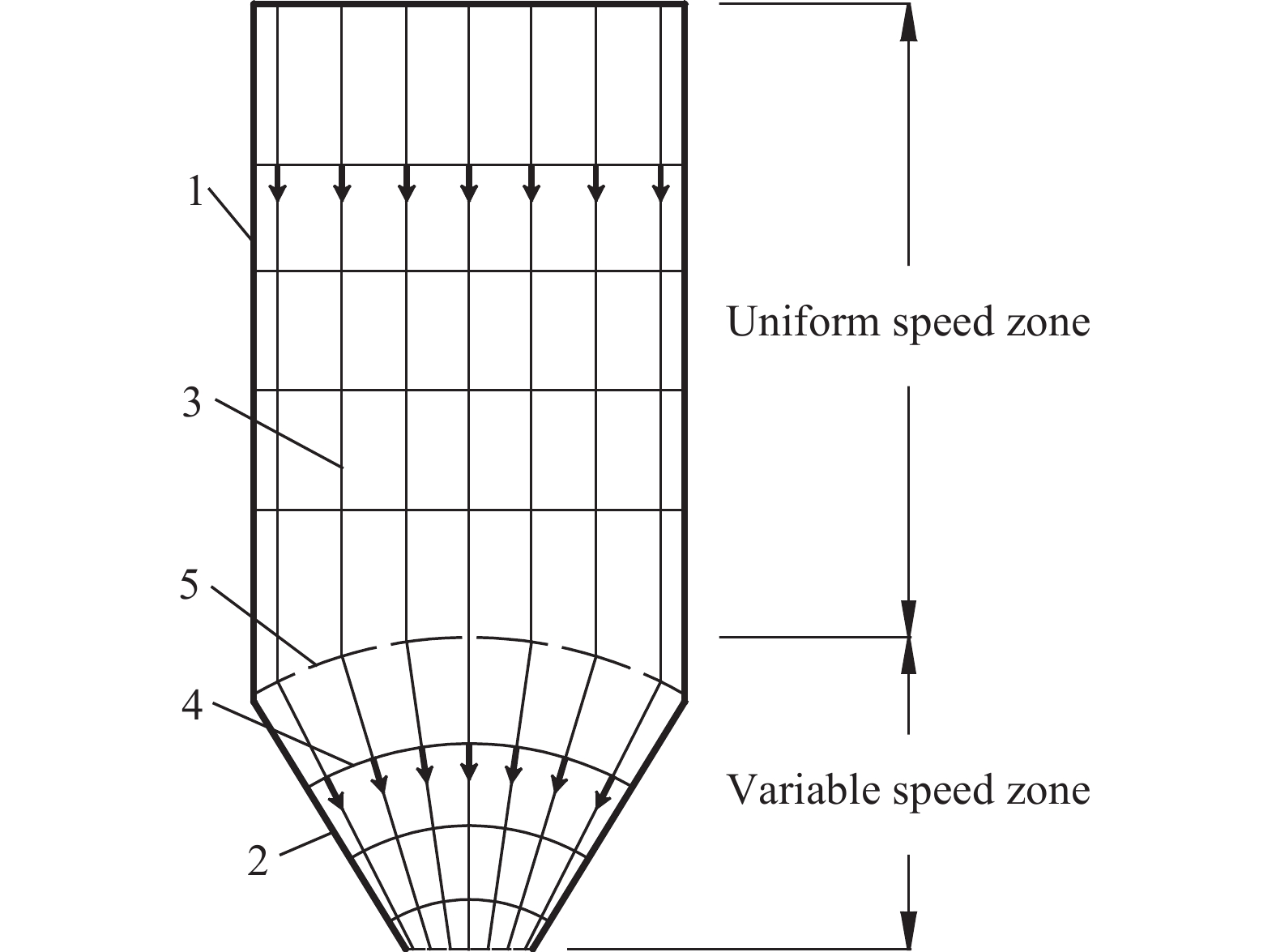
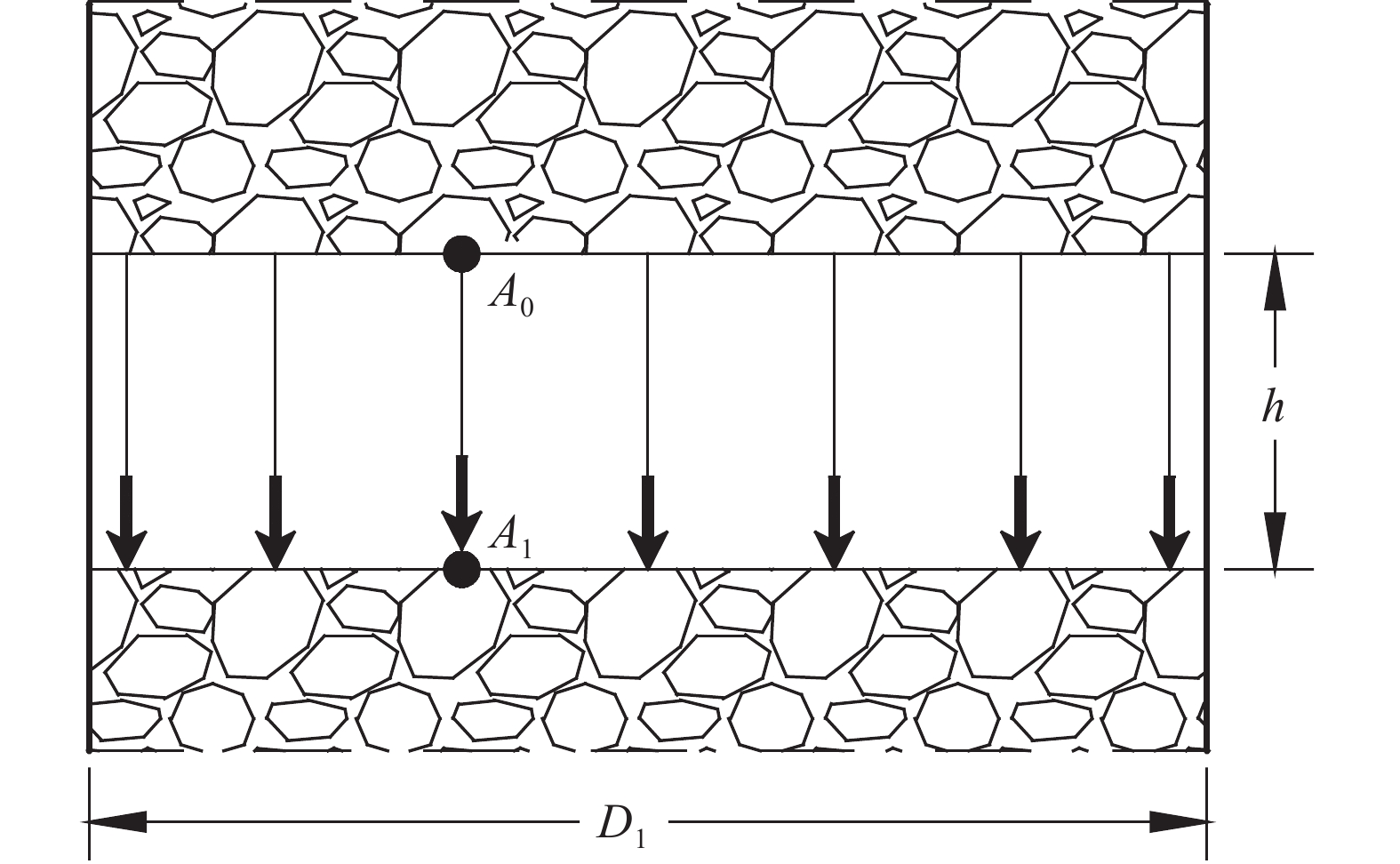
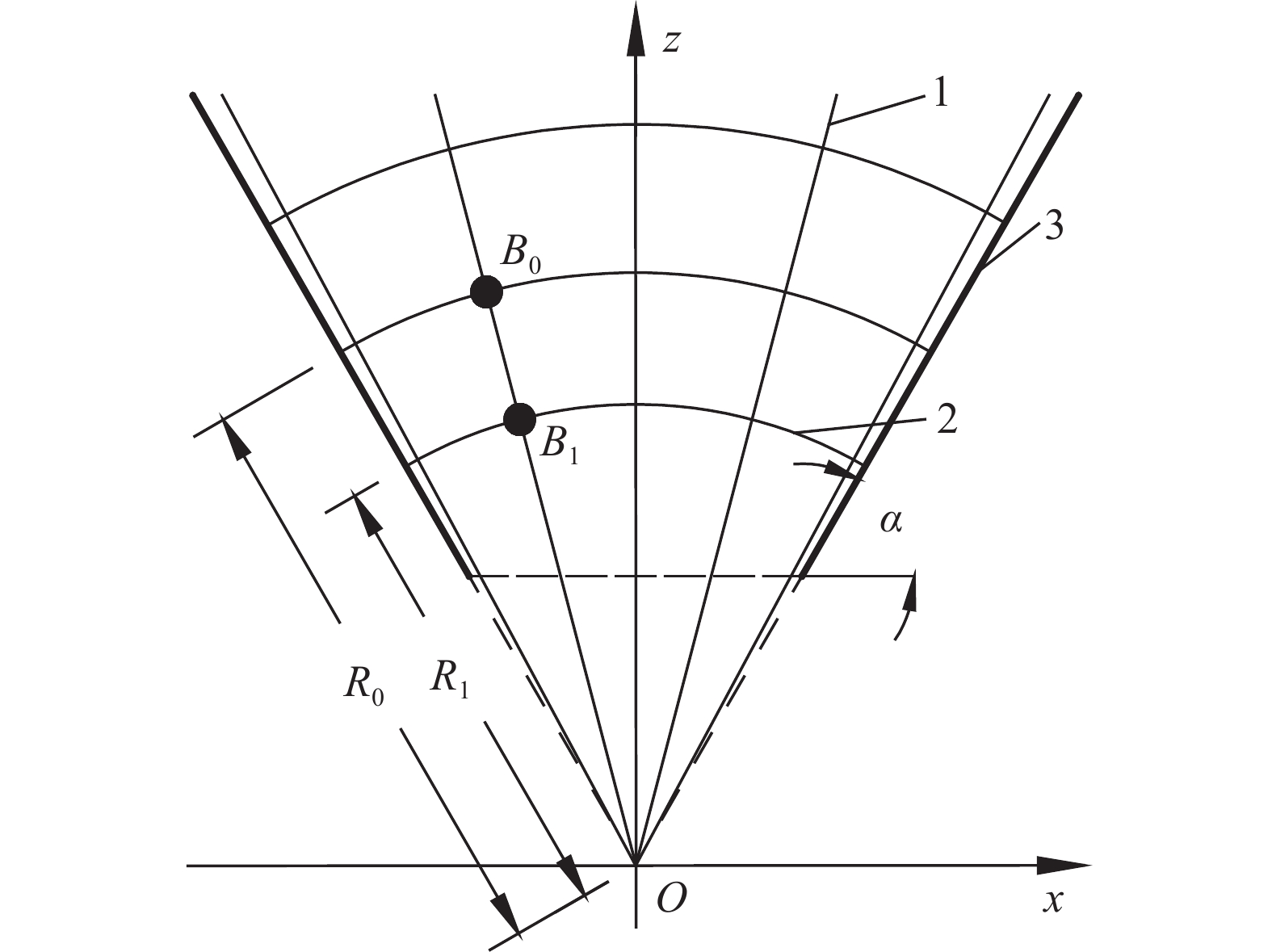
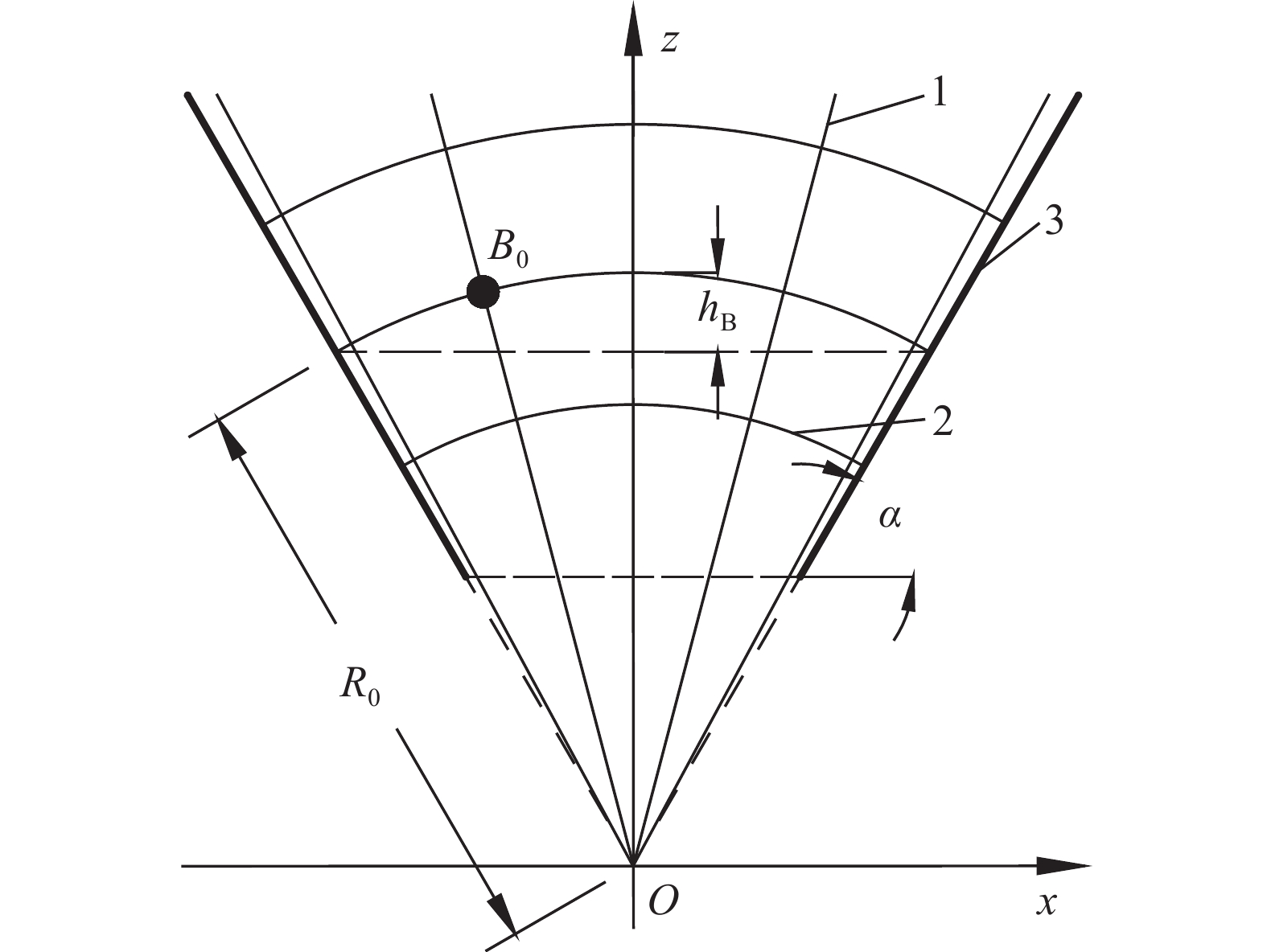
摘要: 為準確預測溜井儲礦段內礦巖散體運移狀態，以放礦漏斗中心線與溜井中心線重合的溜井結構為研究對象，建立了溜井儲礦段礦巖運移軌跡和速度預測模型。首先，根據筒倉卸載過程中顆粒運動特點和理想流體流動單元流動特點的相似性，分析儲礦段內礦巖運移規律；其次，引用流動網絡概念和Beverloo經驗公式，建立了儲礦段礦巖運移網絡，分析了儲礦段礦巖運動截面與礦巖運移速度的關系；最后，在一定的假設條件下，根據流線和等位面分布特征，建立了礦巖位移、運移軌跡和速度方程。研究結果表明：（1）礦巖進入儲礦段后依次經過勻速區、變速區，分別進行勻速直線下向運動、變速曲線運動；（2）當放礦口傾角較小時存在平衡區，該區域下礦巖不發生位移，導致“空環效應”；（3）單位時間內放出礦巖質量和穿過同一等位面的礦巖質量相等。所建立的預測模型表明，勻速區內礦巖運移狀態與儲礦段和放礦口斷面直徑、礦巖粒徑等有關，變速區內礦巖運移狀態還與礦巖所處位置、放礦口傾角等有關。Abstract: For the accurate prediction of the migration state of ore-rock dispersions in the ore pass storage section, a prediction model of an ore pass trajectory and velocity was established by taking the orepass structure, which coincided the centerlines of the ore drawing funnel, and the orepass as the research objects. First, during the silo unloading process, the movement law of ore-rock dispersions in the ore-storage section was analyzed according to the similarity of the particles’ movement characteristics and the flow characteristics of an ideal fluid flow unit. Next, the ore-rock migration network was established based from the flow network concept and the Beverloo empirical formula. Analysis was then conducted on the relationship between the section and the velocity of the ore-rock movement in the ore-storage section of ore pass. Finally, under certain assumed conditions, the displacement equation, the migration trajectory, and the velocity of the ore-rock moving in the ore-storage section were established according to the distribution characteristics of streamline and equipotential surface. Results reveal that after entering the ore-storage section of the ore pass, the ore-rock will pass through two speed zones: (1) a uniform speed zone leading to a uniform linear downward motion and (2) a variable speed zone leading to a variable speed curve motion. When the dip angle of the ore draw-hole is small, an “empty ring effect” is achieved, where no displacement of the lower ore-rock is observed. Finally, the quality of the ore-rock drawing-out in a unit time is found to be equal to that of the ore-rock passing through the same equipotential surface. The predicting model reveals the dependency of the ore-rock migration state in the uniform speed zone with a number of parameters such as the diameter of the section of ore-storage and ore-discharge, ore-rock particle size. Conversely, the ore-rock migration state in the variable speed zone is mainly related to the ore-rock’s location and the inclination angle of ore draw-hole.
-
Key words:
- predicting model /
- ore-rock dispersions /
- migration law /
- trajectory /
- velocity /
- storage section of orepass
-
圖 1 筒倉卸載過程中顆粒運動跡線（1—筒倉邊界；2—放出口；3—顆粒運動跡線；4—卸料死區）
Figure 1. Particle movement trace during the silo unloading (1—the boundary of the silo; 2—ore draw hole; 3—particle movement trajectory; 4—discharge dead zone)
圖 2 直流管中理想流體流動特征（1—直流管邊界; 2—放出口; 3—流動單元運動跡線）
Figure 2. Ideal fluid flow characteristics in a straight pipe (1—boundary of straight pipe; 2—ore draw hole; 3—movement trajectory of flow unit)
圖 3 流動網絡（1—邊界；2—流線；3—等位線）
Figure 3. Flow network (1—boundary; 2—streamline; 3—equipotential line)
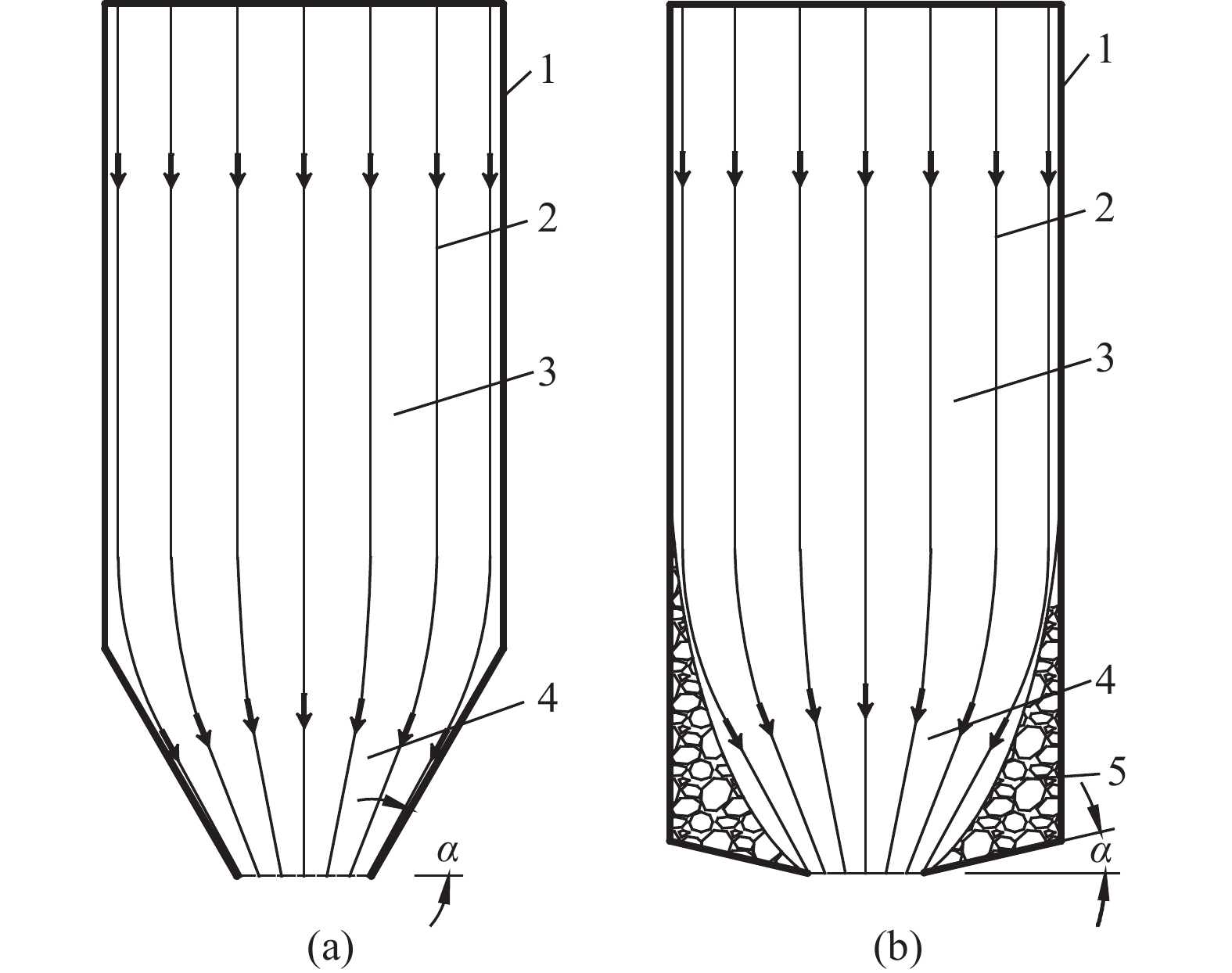
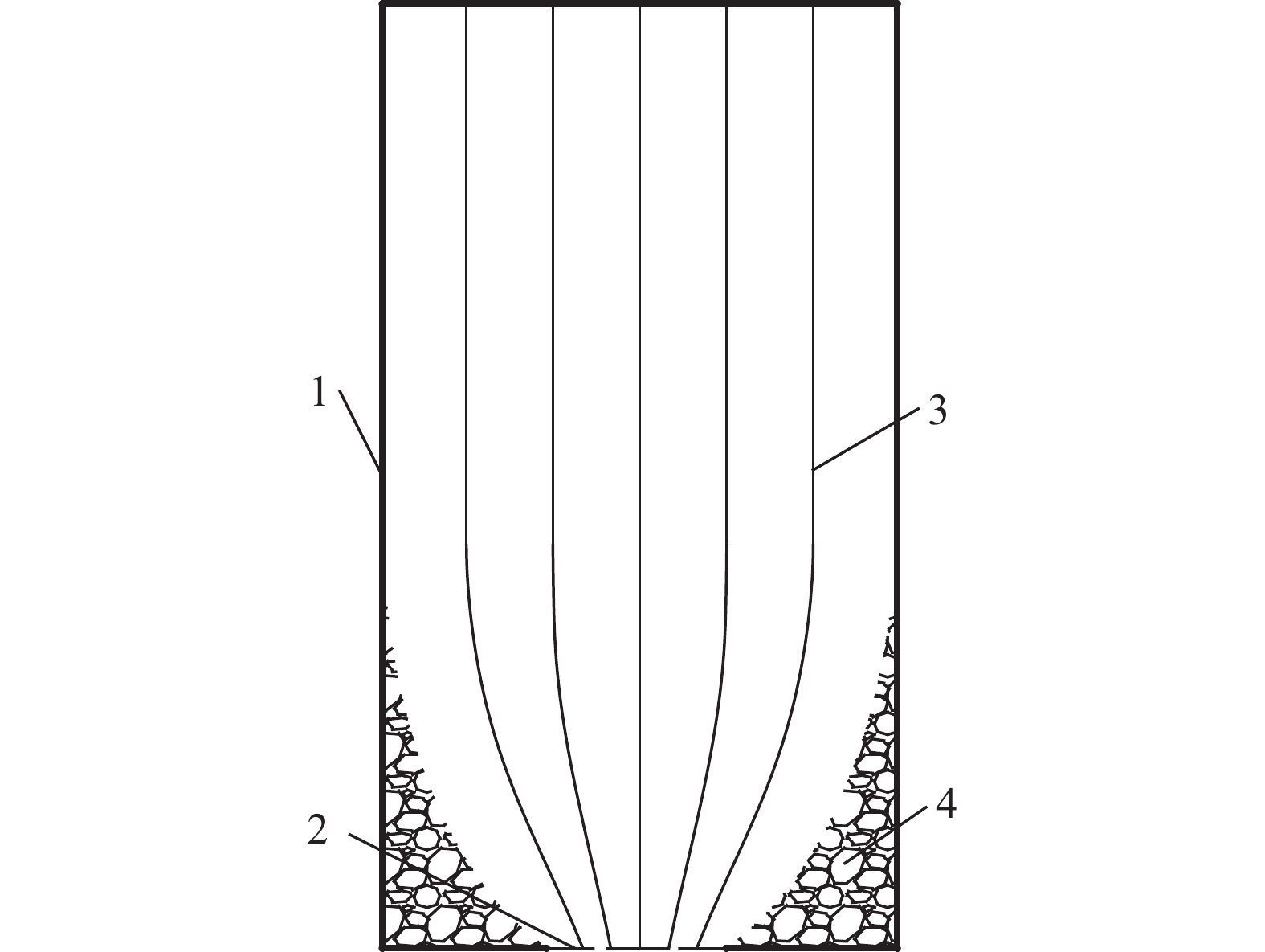
圖 4 溜井儲礦段礦巖運移規律（1—溜井儲礦段邊界；2—流線; 3—礦巖勻速運動區；4—礦巖變速運動區；5—平衡區）。（a）無平衡區時；（b）有平衡區時
Figure 4. Ore-rock migration law in the ore-storage section of orepass (1—boundary of ore-storage section in orepass; 2—streamline; 3—uniform velocity area of ore-rock motion; 4—variable speed area of ore-rock motion; 5—equilibrium area): (a) nonequilibrium area; (b) equilibrium area
圖 5 儲礦段礦巖運移網絡（1—邊界；2—滑動邊界；3—流線；4—等位面；5—分界等位面）
Figure 5. Ore-rock migration network in ore storage section (1—boundary; 2—sliding boundary; 3—streamline; 4—equipotential surface; 5—demarcation equipotential surface)
圖 7 變速區內礦巖運移過程分析（1—流線；2—等位面；3—滑動邊界）
Figure 7. Migration process analysis of ore-rock in variable speed zone (1—streamline; 2—equipotential surface; 3—sliding boundary)
圖 8 儲礦區內礦巖運移過程分析（1—流線；2—等位面；3—滑動邊界）
Figure 8. Analysis on ore-rock moving in the storage section in ore pass (1—streamline; 2—equipotential surface; 3—sliding boundary)
259luxu-164<th id="5nh9l"></th> <strike id="5nh9l"></strike> <th id="5nh9l"><noframes id="5nh9l"><th id="5nh9l"></th> <strike id="5nh9l"></strike> <th id="5nh9l"><noframes id="5nh9l"> <th id="5nh9l"></th> <strike id="5nh9l"><noframes id="5nh9l"><span id="5nh9l"></span> <span id="5nh9l"><noframes id="5nh9l"><span id="5nh9l"></span> <strike id="5nh9l"><noframes id="5nh9l"><strike id="5nh9l"></strike> <span id="5nh9l"><noframes id="5nh9l"> <span id="5nh9l"><noframes id="5nh9l"> <span id="5nh9l"></span> <span id="5nh9l"><video id="5nh9l"></video></span> <th id="5nh9l"><noframes id="5nh9l"><th id="5nh9l"></th> -
參考文獻
[1] Lu Z X, Ma C, Yin Y. Mechanism of deformation and failure on orepass wall under impact and wear. Met Mine, 2018(11): 37路增祥, 馬馳, 殷越. 沖擊磨損作用下的溜井井壁變形破壞機理. 金屬礦山, 2018(11):37 [2] Lu Z X, Ma C, Cao P, et al. Study status and direction of orepass existing problems in metal mine. Met Mine, 2019(3): 1路增祥, 馬馳, 曹朋, 等. 金屬礦山溜井問題研究現狀及方向. 金屬礦山, 2019(3):1 [3] Esmaieli K, Hadjigeorgiou J, Grenon M. Stability analysis of the 19A ore pass at Brunswick mine using a two-stage numerical modeling approach. Rock Mech Rock Eng, 2013, 46(6): 1323 doi: 10.1007/s00603-013-0371-1 [4] Hart R. Case study of the rockpass system at Kloof No. 3 Shaft. J South Afr Inst Min Metall, 2006, 106(1): 1 [5] López-Rodríguez D, Zuriguel I, Maza D. Clogging of granular material in vertical pipes discharged at constant velocity. EPJ Web Conf, 2017, 140: 03033 doi: 10.1051/epjconf/201714003033 [6] Liu Y Z, Zhang B T, Ye Y C, et al. Similarity testing study on characteristics of ore motion and wall damage in mine shaft. J Min Saf Eng, 2018, 35(3): 545劉艷章, 張丙濤, 葉義成, 等. 主溜井礦石運移及井壁破壞特征的相似試驗研究. 采礦與安全工程學報, 2018, 35(3):545 [7] Wei Z C, Zhan S C, Yang S B, et al. Investigation on ore movement and wear of No. 1 orepass in Dexing Copper Mine. Met Mine, 1984(8): 7魏子昌, 占森昌, 楊樹本, 等. 對德興銅礦1號溜井礦石移動規律及其磨損的考察. 金屬礦山, 1984(8):7 [8] Guo B K, Zhang F Z. Characteristics and analysis of ore moving in each area of orepass. Gold, 1985(3): 20郭寶昆, 張福珍. 礦石在溜井各區內的移動特點及其分析. 黃金, 1985(3):20 [9] Tan Z H. A brief discussion on the ore-rock movement in orepass drawing. Met Mine, 1987(2): 24譚志恢. 對溜井放礦礦巖散體運動之淺議. 金屬礦山, 1987(2):24 [10] Wang Q F. Motion Characteristics of Ore and Wearing Characteristics of Wall at Main Ore-Pass in Jinshandian Iron Mine [Dissertation]. Wuhan: Wuhan University of Science and Technology, 2015王其飛. 金山店鐵礦主溜井內礦石運移及井壁磨損特征研究[學位論文]. 武漢: 武漢科技大學, 2015 [11] Sun Q C, Wang G Q. Review on granular flow dynamics and its discrete element method. Adv Mech, 2008, 38(1): 87 doi: 10.3321/j.issn:1000-0992.2008.01.006孫其誠, 王光謙. 顆粒流動力學及其離散模型評述. 力學進展, 2008, 38(1):87 doi: 10.3321/j.issn:1000-0992.2008.01.006 [12] Sun H, Jin A B, Gao Y T, et al. Flow characteristics of caved ore and rock in the multiple draw-point condition. Chin J Eng, 2015, 37(10): 1251孫浩, 金愛兵, 高永濤, 等. 多放礦口條件下崩落礦巖流動特性. 工程科學學報, 2015, 37(10):1251 [13] Chen Q F, Chen Q L, Zhong J Y, et al. Flow pattern of granular ore rock in a single funnel under a flexible isolation layer. Chin J Eng, 2016, 38(7): 893陳慶發, 陳青林, 仲建宇, 等. 柔性隔離層下單漏斗散體礦巖流動規律. 工程科學學報, 2016, 38(7):893 [14] Li T. Study on the Migration Law of Granular Ore-Rock under Draw by Caving Method [Dissertation]. Beijing: University of Science and Technology Beijing, 2018李濤. 崩落法放礦過程中散體礦巖運移規律研究[學位論文]. 北京: 北京科技大學, 2018 [15] Li W, Liu Y Z, Zou X T, et al. Research on distribution characteristics of wall dynamic stress at ore storage section of ore-pass during ore-drawing. Met Mine, 2018(9): 47李偉, 劉艷章, 鄒曉甜, 等. 溜井放礦過程中貯礦段井壁動態應力分布特征研究. 金屬礦山, 2018(9):47 [16] Finnemore E J, Franzini J B. Fluid Mechanics with Engineering Applications. 10th Ed. New York City: McGraw-Hill Science/Engineering/Math, 2001 [17] Williams J C. The rate of discharge of coarse granular materials from conical mass flow hoppers. Chem Eng Sci, 1977, 32(3): 247 doi: 10.1016/0009-2509(77)80202-9 [18] Wu Q S, Hu M B. Advances on dynamic modeling and experimental studies for granular flow. Adv Mech, 2002, 32(2): 250 doi: 10.3321/j.issn:1000-0992.2002.02.009吳清松, 胡茂彬. 顆粒流的動力學模型和實驗研究進展. 力學進展, 2002, 32(2):250 doi: 10.3321/j.issn:1000-0992.2002.02.009 [19] Wang N S. Study on Flow Behaviours of Granular Matter in A Two-Dimensional Channel[Dissertation]. Shanghai: East China University of Science and Technology, 2019王寧生. 二維通道中顆粒物質流動行為研究[學位論文]. 上海: 華東理工大學, 2019 [20] Brown C L, Richards J C. Principles of Powder Mechanics: Essays on the Packing and Flow of Powders and Bulk Solids. Oxford: Pergamon Press, 1970 [21] Zhou Y X. Analysis of the granular pressure and velocity field of hourglass flow based on the local constitutive law. Acta Phys Sin, 2019, 68(13): 224周益嫻. 基于連續數值模擬的筒倉卸載過程中顆粒物壓強及其速度場分析. 物理學報, 2019, 68(13):224 [22] Beverloo W A, Leniger H A, van de Velde J. The flow of granular solids through orifices. Chem Eng Sci, 1961, 15(3-4): 260 doi: 10.1016/0009-2509(61)85030-6 [23] Janda A, Zuriguel I, Maza D. Flow rate of particles through apertures obtained from self-similar density and velocity profiles. Phys Rev Lett, 2012, 108(24): 248001 doi: 10.1103/PhysRevLett.108.248001 [24] Benyamine M, Aussillous P, Dalloz-Dubrujeaud B. Discharge flow of a granular media from a silo: effect of the packing fraction and of the hopper angle. EPJ Web Conf, 2017, 140: 03043 doi: 10.1051/epjconf/201714003043 [25] Hibbeler R C. Dynamics. Translated by Li J F, Yuan C Q, Lü J. Beijing: Mechanical Industry Press, 2014希伯勒 R C. 動力學. 李俊峰, 袁長清, 呂敬, 譯. 北京: 機械工業出版社, 2014 -
下載:
點擊查看大圖
計量
- 文章訪問數: 1198
- HTML全文瀏覽量: 589
- PDF下載量: 58
- 被引次數: 0
