循環擾動荷載作用下花崗巖中裂隙萌生擴展過程的顆粒流模擬

張杰; 郭奇峰; 蔡美峰; 張英; 汪炳鋒; 吳星輝

doi:10.13374/j.issn2095-9389.2020.03.15.003

循環擾動荷載作用下花崗巖中裂隙萌生擴展過程的顆粒流模擬

doi: 10.13374/j.issn2095-9389.2020.03.15.003

張杰^{1, 2},
郭奇峰^{1, 2, ,},
蔡美峰^{1, 2},
張英^{1, 2},
汪炳鋒^{1, 2},
吳星輝^{1, 2}

1.
北京科技大學土木與資源工程學院，北京 100083
2.
北京科技大學金屬礦山高效開采與安全教育部重點實驗室，北京 100083

基金項目: 中央高校基本科研業務費資助項目（FRF-TP-18-015A3）；國家自然科學基金資助項目（51974014，U2034206）

詳細信息

通訊作者:
E-mail：guoqifeng@ustb.edu.cn

中圖分類號: TD315.3
計量
- 文章訪問數: 2605
- HTML全文瀏覽量: 700
- PDF下載量: 117
- 被引次數: 0
出版歷程
- 收稿日期: 2020-03-15
- 刊出日期: 2021-05-25

Particle flow simulation of the crack propagation characteristics of granite under cyclic load

ZHANG Jie^{1, 2},
GUO Qi-feng^{1, 2
, ,},
CAI Mei-feng^{1, 2},
ZHANG Ying^{1, 2},
WANG Bing-feng^{1, 2},
WU Xing-hui^{1, 2}

1.
School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China
2.
Key Laboratory of Ministry of Education of China for High-Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing 100083, China

More Information

Corresponding author: E-mail: guoqifeng@ustb.edu.cn

摘要

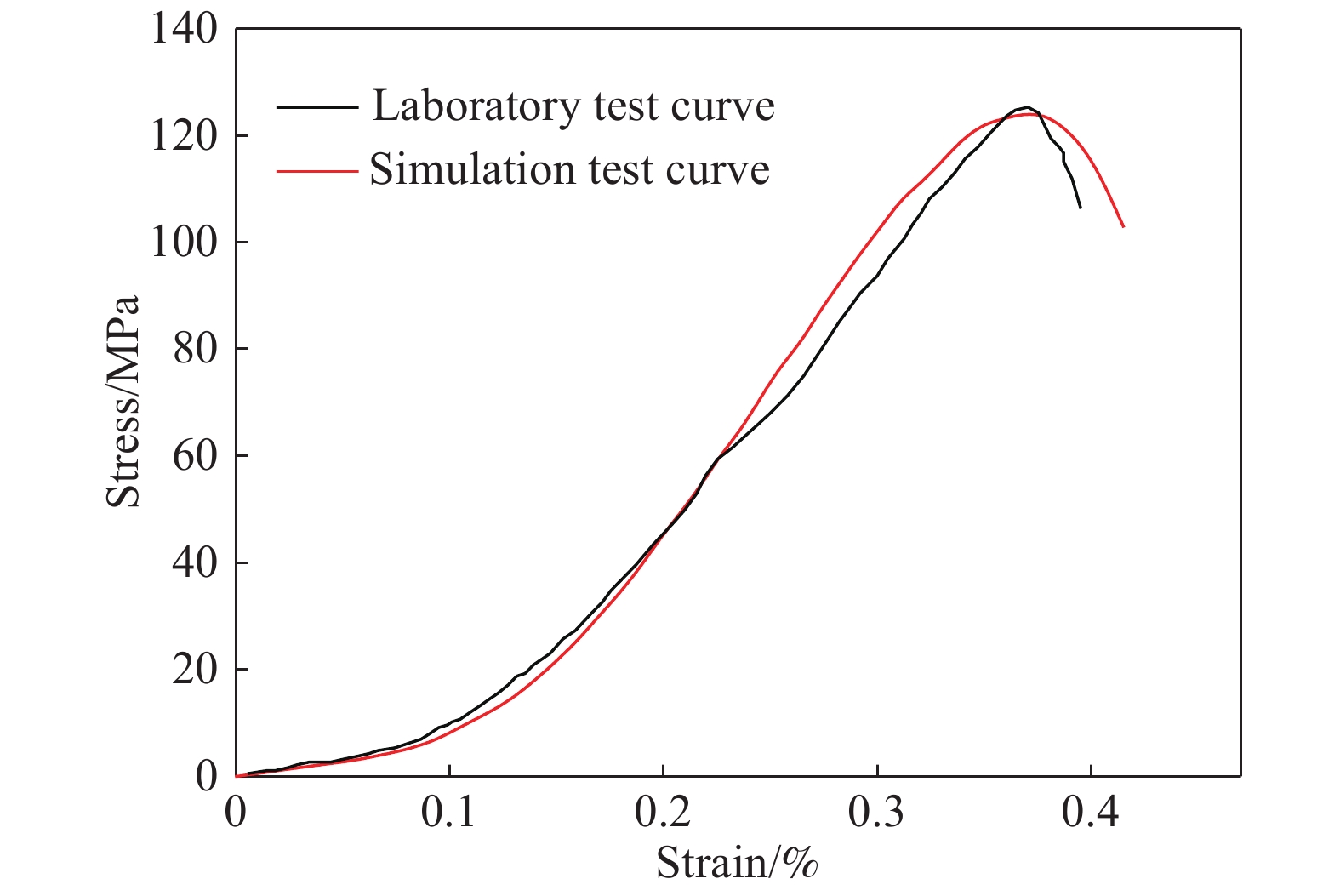
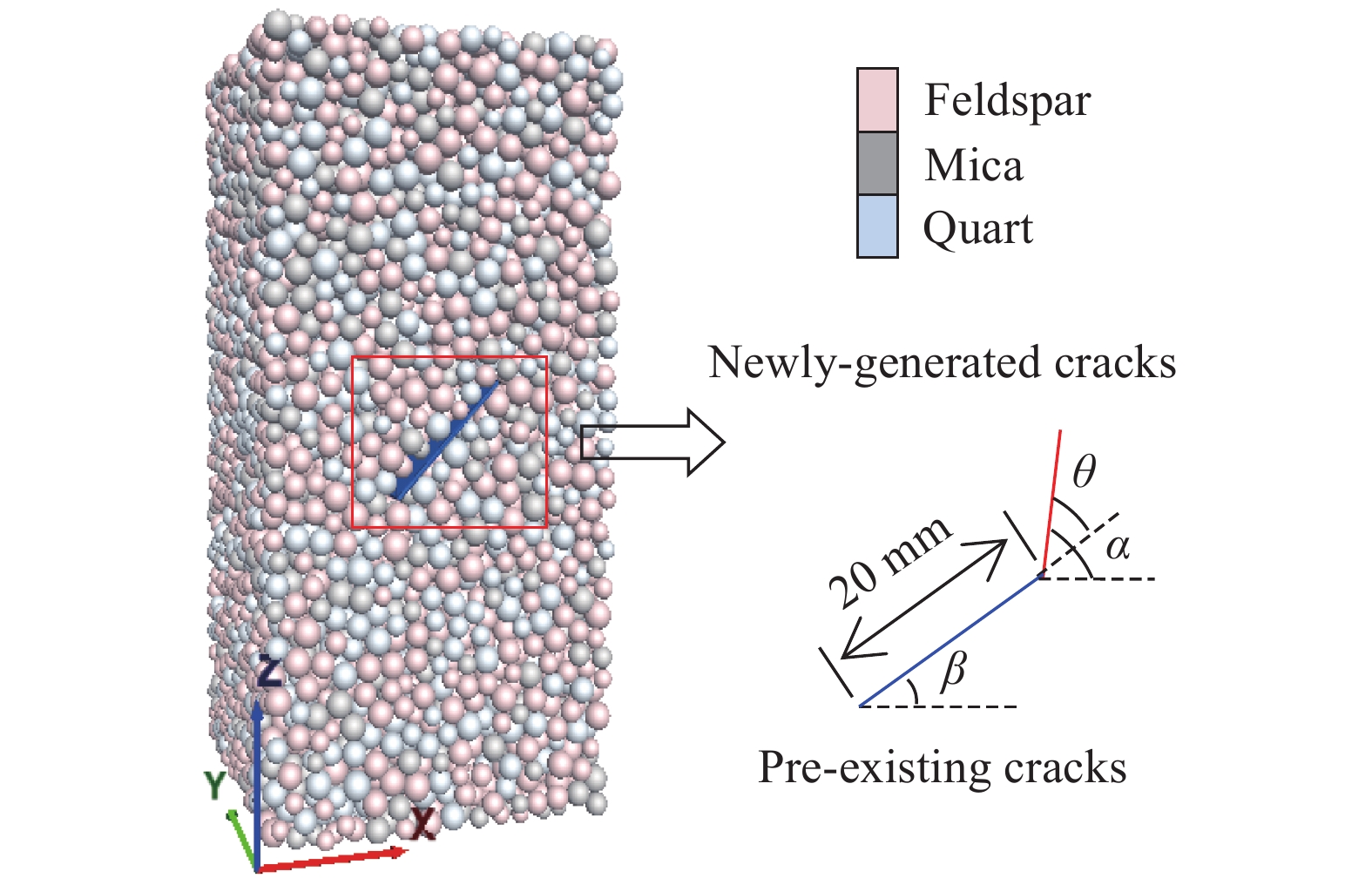
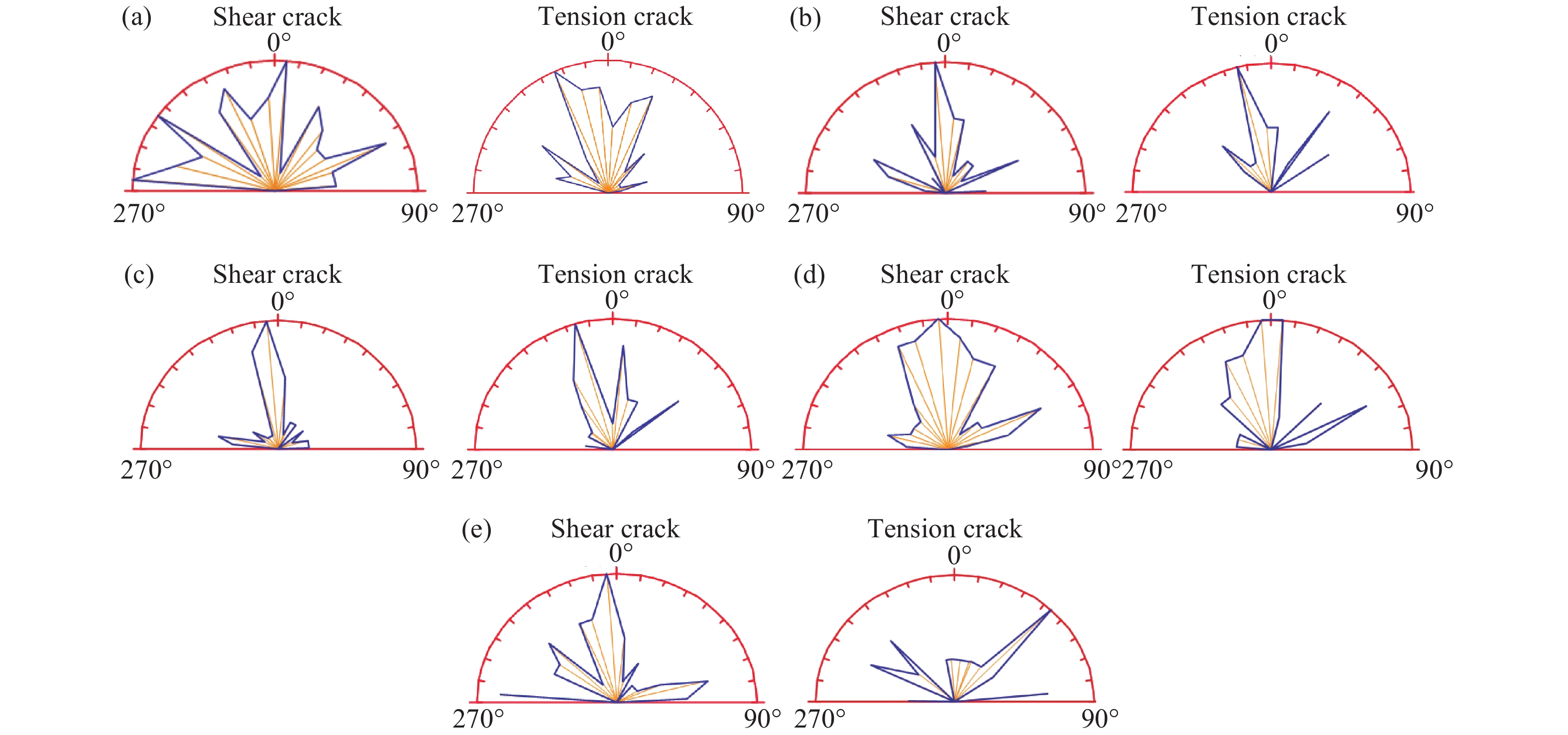
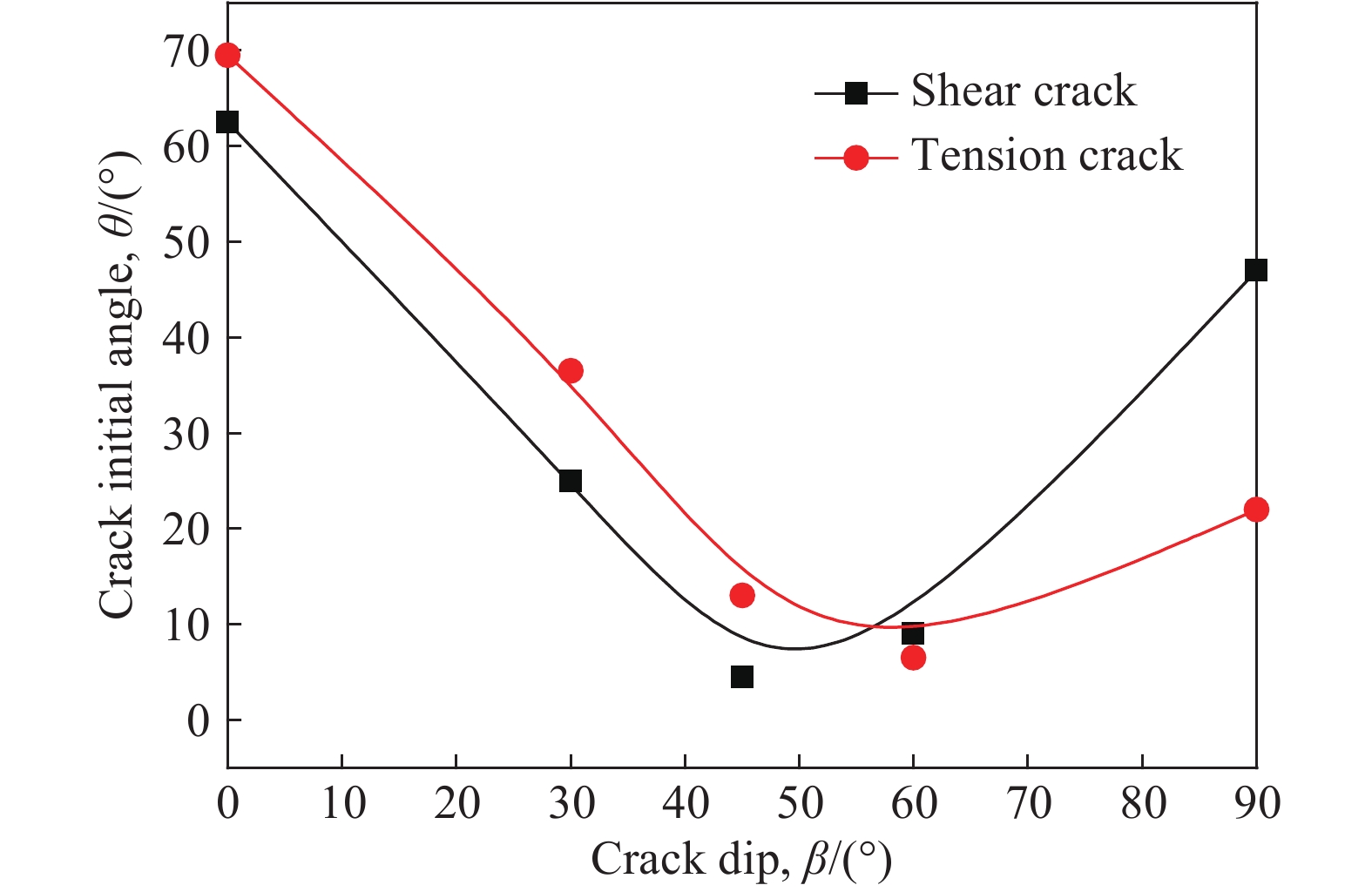
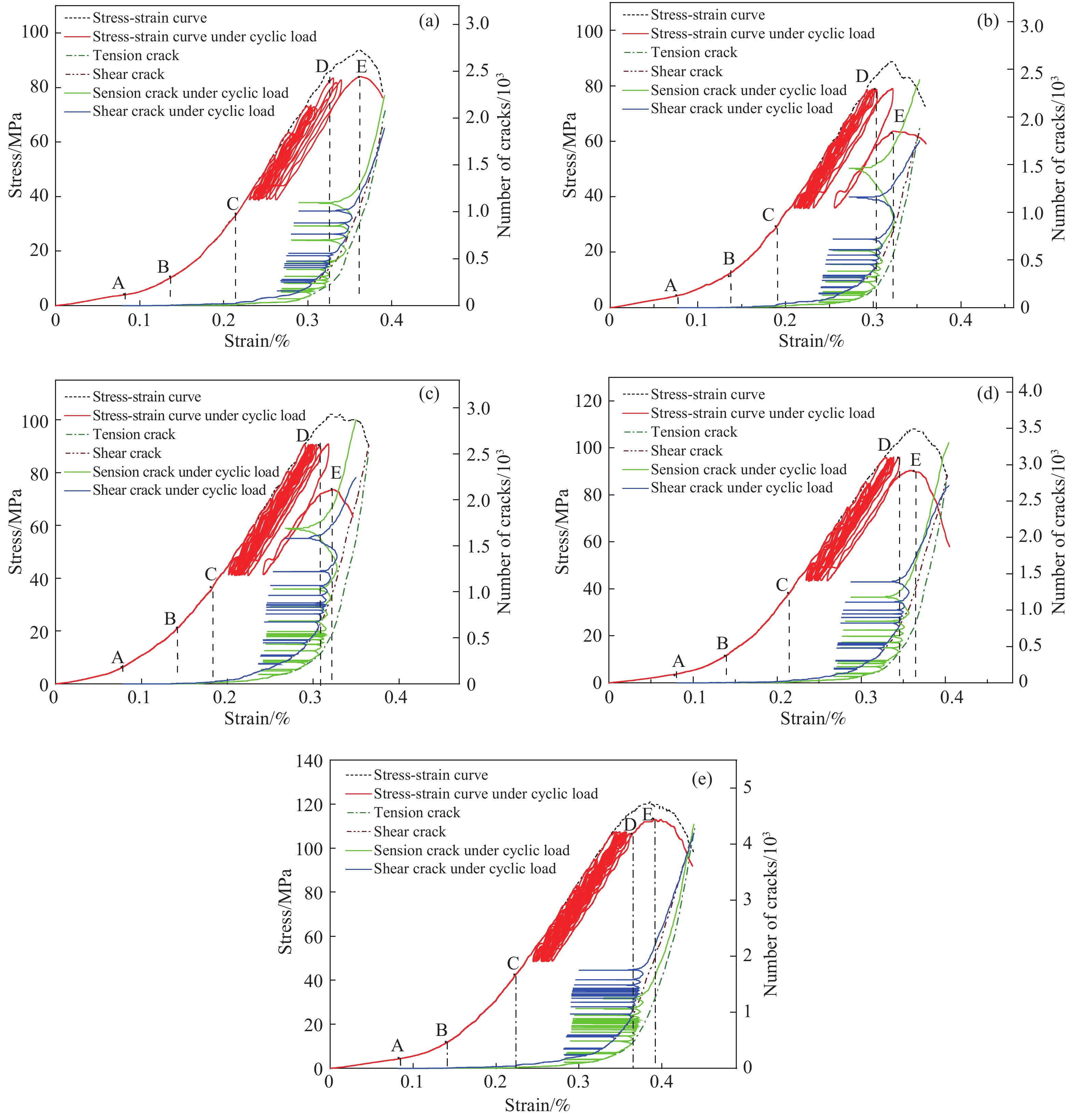
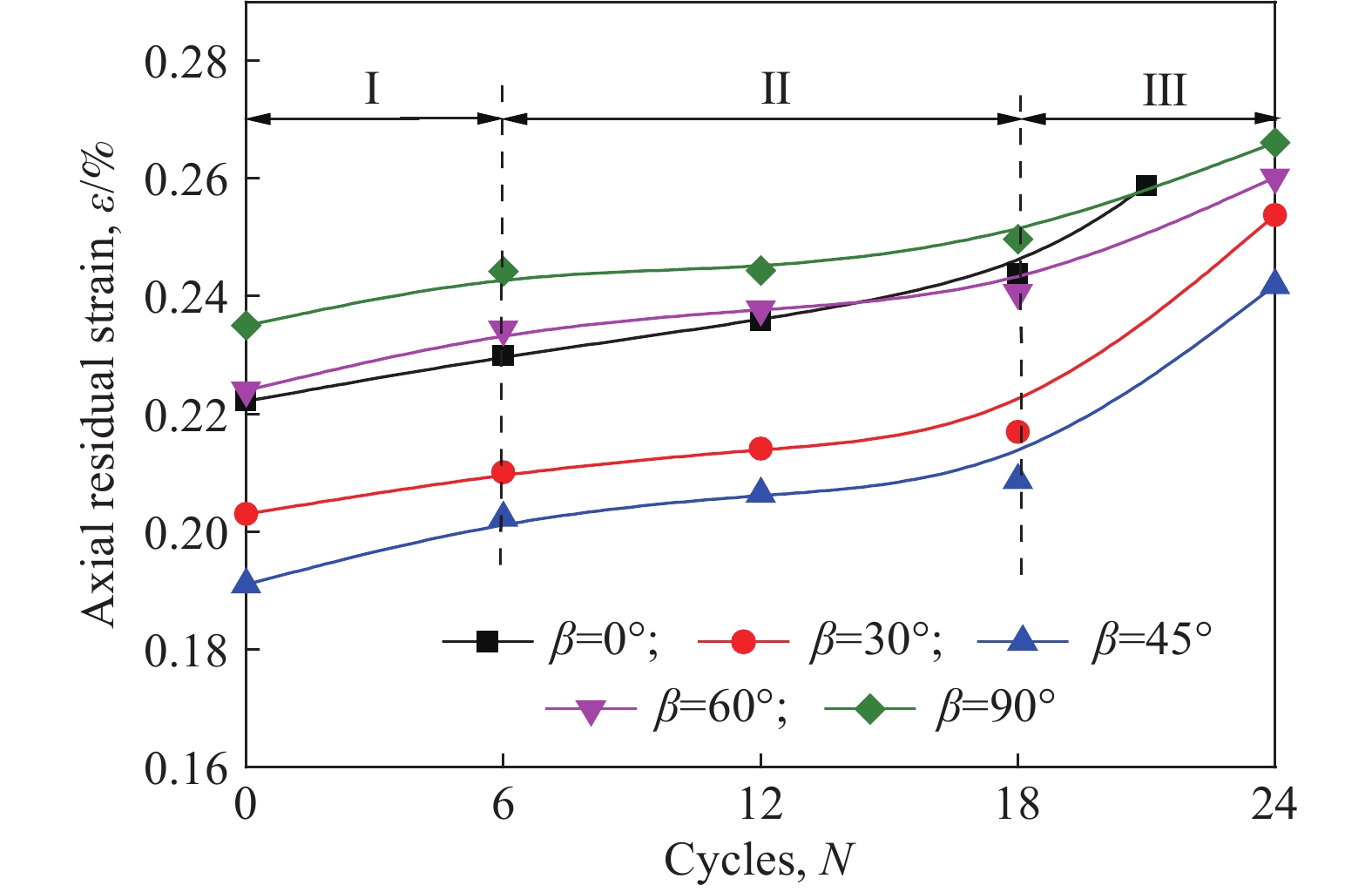
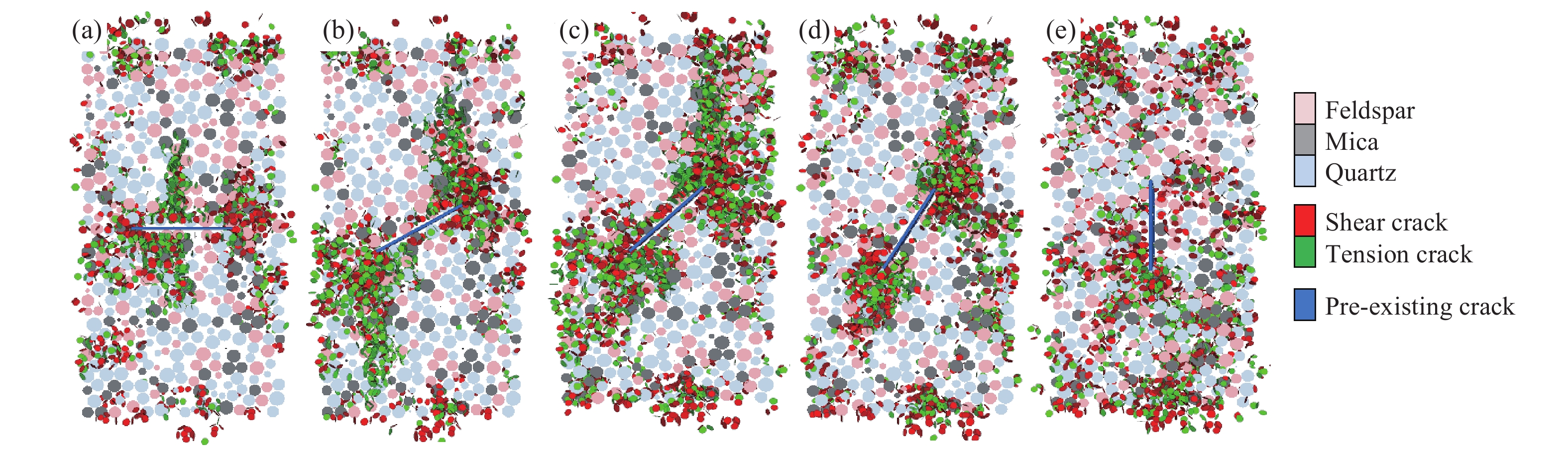
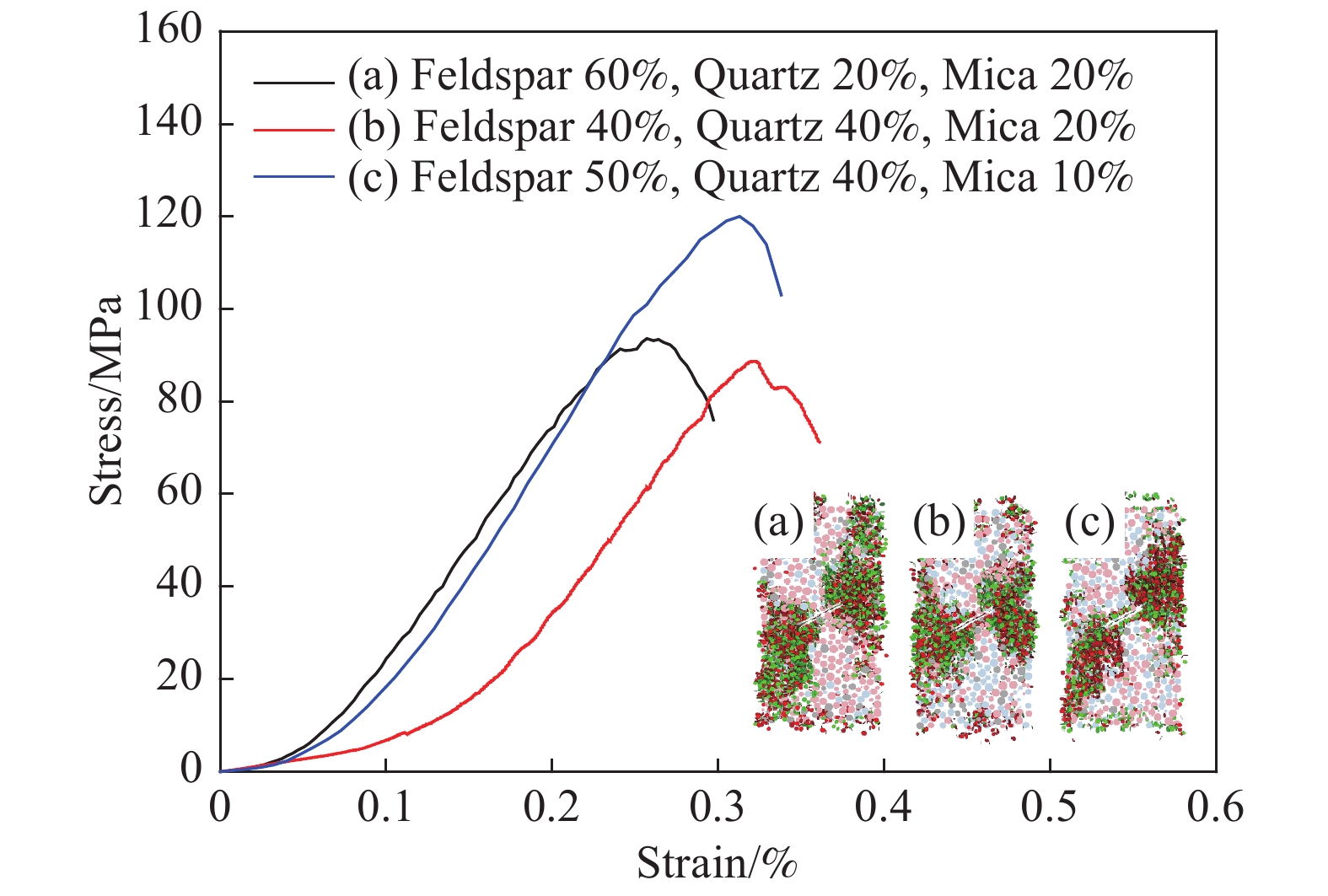
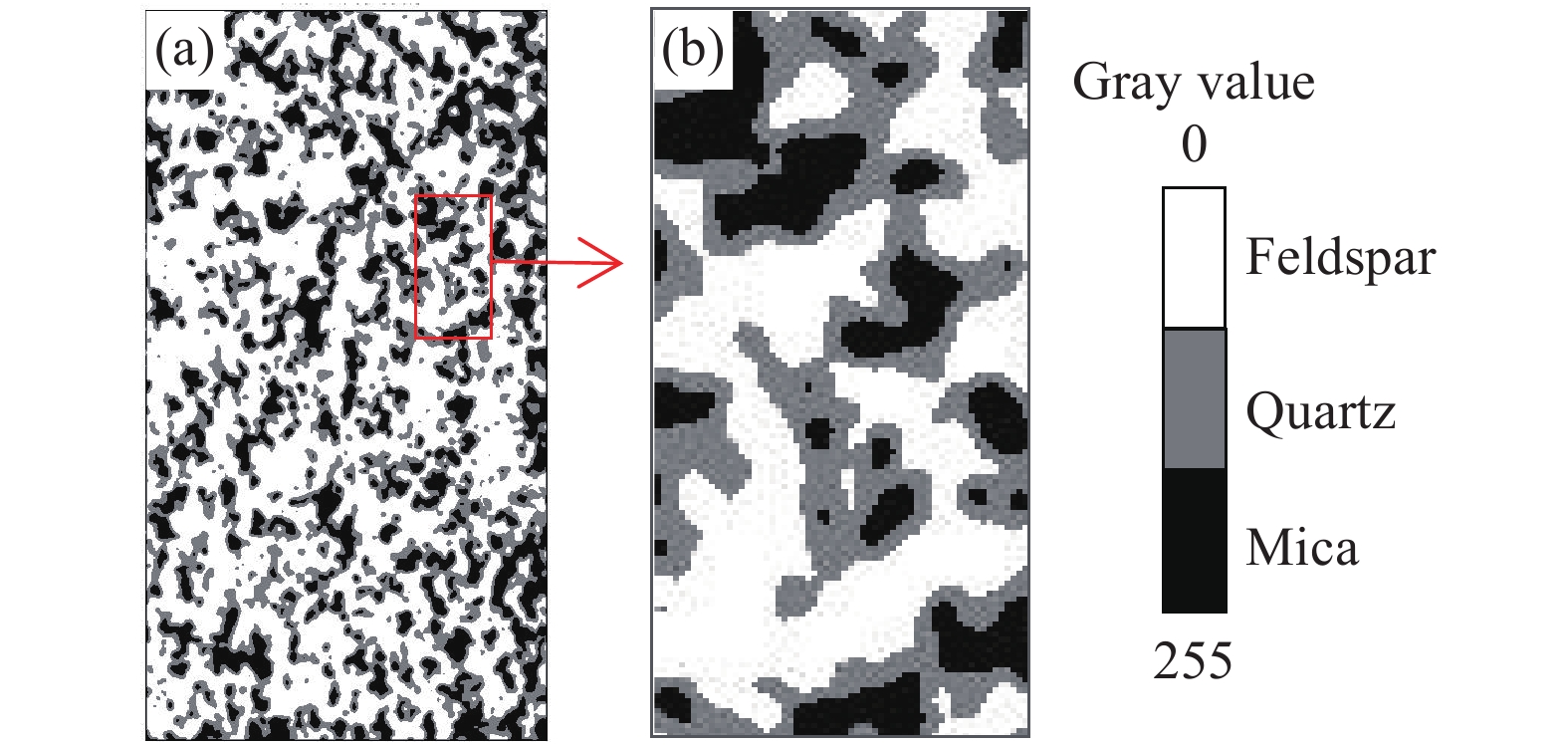
摘要: 從細觀角度、采用顆粒離散元法開展了預制裂隙花崗巖循環加卸載的數值模擬試驗。首先，使用圖像處理技術識別花崗巖中的不同細觀組分、結合室內單軸壓縮試驗結果對細觀力學參數進行了標定。然后，通過編制顆粒流代碼追蹤裂隙的類型和擴展過程，分析巖石破壞過程中裂隙發展的階段性特征。結果表明：不同傾角裂隙巖石的新生裂隙走向與預制裂隙貫通方向基本一致；根據新生裂隙的優勢傾向分組得到裂隙起裂角與預制裂隙傾角的關系：傾角β≤45°時剪切和張拉裂隙的起裂角單調遞減，傾角β≥60°時剪切和張拉裂隙的起裂角單調遞增；循環擾動荷載增加了裂隙巖體的軸向變形，軸向累積殘余應變曲線呈反S形、提高擾動荷載應力上限促使曲線進入加速階段；試件峰值強度隨裂隙傾角增大表現出先減小后增大的趨勢，峰值強度為實驗室完整巖石單軸抗壓強度的63% ~ 89%，反映了較為明顯的劣化現象；在循環荷載作用下，剪切裂隙和張拉裂隙增長曲線表現出明顯的變化特點，在裂隙不穩定擴展階段中張拉裂隙數目增長速率顯著大于剪切裂隙，對分析巖石變形破壞過程具有一定的參考意義。
- 細觀結構 /
- 循環擾動 /
- 裂隙產狀 /
- 裂隙擴展 /
- 顆粒流
Abstract: The microcracks in natural rock masses considerably impact the stability of the underground engineering structures. The mechanical properties of the cracked rock masses contribute considerably to the strength of the rock masses and their compression failure mechanism. The instability and failure of the surrounding rocks are often induced by the propagation and penetration of these internal cracks. In practical engineering, rock mass excavation is a process involving dynamic disturbance. The mechanical properties of the rocks under cyclic load are considerably different from those of the rocks under static load. The characteristics and development of microcracks are the main factors influencing rock fatigue failure. From the microscopic viewpoint, the particle-based discrete element method is used to conduct the cyclic loading and unloading tests of the preexisting cracked granite. First, the microcompositions of granite are determined using image processing techniques, and the micromechanical parameters are calibrated based on the indoor uniaxial compression test results. The stage of crack development during rock failure is analyzed by compiling particle flow code to track the type and propagation process of cracks. Results indicate that the orientations of new cracks in fractured rocks with different dip angles are similar to those of the preexisting cracks. Further, the relation between the crack initiation angle and the inclination angle of the preexisting cracks is obtained according to the tendency of new cracks. The crack initiation angle of shear and tension cracks decreases and increases monotonically, respectively, when the inclination angle β ≤ 45° and β ≥ 60°. The cyclic disturbance load increases the axial deformation of the fractured rock mass, and the axial cumulative residual strain curve exhibits an inverse S-shape when entering the acceleration stage faster with the increasing upper stress limit. The peak strength of the model specimen shows a decreasing trend followed by an increasing trend with the increasing fracture inclination. The peak strengths of the laboratory-intact rock are 63% to 89%, indicating an obvious deterioration phenomenon in the rock materials. The growth of shear and tension cracks show different characteristics under cyclic load; the growth rate of tension cracks is considerably higher than that of shear cracks during the unstable crack development stage. The results presented in this study may be used as reference to investigate the deformation and failure mechanisms of rock materials.
- microstructure /
- cyclic load /
- crack orientation /
- crack propagation /
- particle flow

HTML全文

圖 1 花崗巖圖像礦物識別。（a）標準試件；（b）局部放大圖

Figure 1. Mineral recognition from a granite image: (a) standard test specimen; (b) partial enlarged detail

下載: 全尺寸圖片幻燈片

圖 2 試件應力–應變曲線

Figure 2. Stress–strain curves of a specimen

下載: 全尺寸圖片幻燈片

圖 3 裂隙花崗巖試件模型

Figure 3. Numerical model of a granite specimen with a single crack

下載: 全尺寸圖片幻燈片

圖 4 裂隙巖石試件走向玫瑰花圖。（a）β = 0°；（b）β = 30°；（c）β = 45°；（d）β = 60°；（e）β = 90°

Figure 4. Strike rose diagrams of a cracked rock specimen: (a) β = 0°; (b) β = 30°; (c) β = 45°; (d) β = 60°; (e) β = 90°

下載: 全尺寸圖片幻燈片

圖 5 預制裂隙傾角β與起裂角θ的關系

Figure 5. Relation between the crack initial angle θ and crack dip β

下載: 全尺寸圖片幻燈片

圖 6 新生裂隙數目與軸向應變的變化情況。（a）β = 0°；（b）β = 30°；（c）β = 45°；（d）β = 60°；（e）β = 90°

Figure 6. Number of newly generated cracks and the change in axial strain: (a) β = 0°; (b) β = 30°; (c) β = 45°; (d) β = 60°; (e) β = 90°

下載: 全尺寸圖片幻燈片

圖 7 循環次數與軸向應變關系

Figure 7. Relation between the number of cycles and axial strain

下載: 全尺寸圖片幻燈片

圖 8 不同預制裂隙傾角巖石試件的破裂模式。（a）β =0°；（b）β =30°；（c）β =45°；（d）β =60°；（e）β =90°

Figure 8. Fracture modes of a rock specimen with different crack angles: (a) β = 0°; (b) β = 30°; (c) β = 45°; (d) β = 60°; (e) β = 90°

下載: 全尺寸圖片幻燈片

圖 9 不同礦物比例的巖石應力–應變曲線和破壞模式

Figure 9. Stress–strain curves and failure modes of rocks with different mineral ratios

下載: 全尺寸圖片幻燈片

表 1 花崗巖細觀力學性質參數

Table 1. Microscale mechanical parameters of granite

Mineral component	Particles forming grains				Linear parallel bond model
Mineral component	Minimum particle radius forming grain, R_min/mm	Maximum to minimum radius ratio, R_max/R_min	Young’s modulus, E_c/GPa	Ratio of normal to shear stiffness of the particle, k_n/k_s	Young’s modulus, $ {\bar E_{\rm{c}}} $/GPa	Ratio of normal to shear stiffness of the parallel bond, ${\bar k_{\rm{n}}} $/$ {\bar k_{\rm{s}}} $	Shear bond strength, $ {\tau _{\rm{c}}} $/MPa	Friction ratio, $ \bar \varphi $	Tensile–shear bond strength ratio, ${\bar \sigma _{\rm{c}}} $/$ {\bar \tau _{\rm{c}}} $
Feldspar	1.2	1.66	45.5	1.15	28.0	1.6	51.0	0.5	1.0
Quartz	1.2	1.66	33.0	1.15	22.6	1.6	81.6	0.8	1.0
Mica	1.2	1.66	11.2	1.15	5.9	1.6	15.3	0.15	1.0

下載: 導出CSV

表 2 新生裂隙傾向和傾角分布統計

Table 2. Statistics of the distribution of tendencies and inclinations for newly generated cracks

Tendencies and inclinations for preexisting cracks	Shear cracks			Tension crack
Tendencies and inclinations for preexisting cracks	Tendency grouping	Average inclination/(°)	Percentage/%	Tendency grouping	Average inclination/(°)	Percentage/%
90°∠0°	151°–160°	65	6.3	61°–70°	77	8.0
90°∠0°	211°–220°	60	6.3	251°–260°	62	8.0
90°∠30°	261°–270°	62	11.9	71°–80°	61	10.5
90°∠30°	241°–250°	48	9.5	141°–150°	72	10.5
90°∠45°	261°–270°	54	17.4	71°–80°	52	18.5
90°∠45°	251°–260°	45	15.2	91°–100°	64	11.1
90°∠60°	261°–270°	51	9.5	81°–90°	64	14.3
90°∠60°	251°–260°	51	7.9	61°–70°	69	10.7
90°∠90°	261°–270°	45	8.5	131°–140°	88	11.1
90°∠90°	181°–190°	43	6.4	21°–30°	48	5.6

下載: 導出CSV

表 3 峰值強度統計

Table 3. Statistics of peak strengths

Inclination angle of rock specimen, β/(°)	Peak strength under cyclic load/MPa	Peak strength under cyclic load to the uniaxial strength of the intact rock ratio	Cycles
0	84.4	0.67	21
30	79.3	0.63	24
45	91.3	0.73	24
60	96.7	0.77	24
90	112	0.89	24

下載: 導出CSV

259luxu-164

參考文獻(32)

[1]	Lajtai E Z, Carter B J, Ayari M L. Criteria for brittle fracture in compression. Eng Fract Mech, 1990, 37(1): 59 doi: 10.1016/0013-7944(90)90331-A
[2]	Yang S Q, Jing H W, Wang S Y. Experimental investigation on the strength, deformability, failure behavior and acoustic emission locations of red sandstone under triaxial compression. Rock Mech Rock Eng, 2012, 45(4): 583 doi: 10.1007/s00603-011-0208-8
[3]	Cao P, Liu T Y, Pu C Z, et al. Crack propagation and coalescence of brittle rock-like specimens with pre-existing cracks in compression. Eng Geol, 2015, 187: 113 doi: 10.1016/j.enggeo.2014.12.010
[4]	Chen W Z, Li S C, Zhu W S, et al. Experimental and numerical research on crack propagation in rock under compression. Chin J Rock Mech Eng, 2003, 22(1): 18 doi: 10.3321/j.issn:1000-6915.2003.01.003 陳衛忠, 李術才, 朱維申, 等. 巖石裂紋擴展的實驗與數值分析研究. 巖石力學與工程學報, 2003, 22(1):18 doi: 10.3321/j.issn:1000-6915.2003.01.003
[5]	Zhao H J, Dwayne T, Guo J, et al. Numerical study on fracture propagation and interaction using continuous-discontinuous failure method. J Eng Geol, 2019, 27(5): 933 趙海軍, Dwayne T, 郭捷, 等. 基于連續-非連續方法的裂隙破壞與相互作用研究. 工程地質學報, 2019, 27(5):933
[6]	Song Y Q, Li M, Wang X, et al. Experimental test on marble containing two pre-existing cracks under loading and unloading conditions based on high-speed photography. Chin J Rock Mech Eng, 2015, 34(Suppl 1): 2679 宋彥琦, 李名, 王曉, 等. 基于高速攝影的雙預制裂紋大理巖加卸載試驗. 巖石力學與工程學報, 2015, 34(增刊 1):2679
[7]	Guo Q F, Wu X, Cai M F, et al. Experiment on the strength characteristics and failure modes of granite with pre-existing cracks. Chin J Eng, 2019, 41(1): 43 郭奇峰, 武旭, 蔡美峰, 等. 預制裂隙花崗巖的強度特征與破壞模式試驗. 工程科學學報, 2019, 41(1):43
[8]	Guo Q F, Pan J L, Cai M F, et al. Investigating the effect of rock bridge on the stability of locked section slopes by the direct shear test and acoustic emission technique. Sensors, 2020, 20(3): 638 doi: 10.3390/s20030638
[9]	Tang L Z, Song Y L. Particle flow simulation of macro- and meso-mechanical properties of uniaxially compressed rock-like specimens with non-coplanar overlapping flaws. Chin J Rock Mech Eng, 2019, 38(11): 2161 唐禮忠, 宋徉霖. 含非共面重疊型微裂隙類巖石試樣單軸受壓宏細觀力學特性顆粒流模擬. 巖石力學與工程學報, 2019, 38(11):2161
[10]	Martin C D, Chandler N A. The progressive fracture of Lac du Bonnet granite. Int J Rock Mech Min Sci Geomech Abstr, 1994, 31(6): 643 doi: 10.1016/0148-9062(94)90005-1
[11]	Cai M, Kaiser P K, Tasaka Y, et al. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int J Rock Mech Min Sci, 2004, 41(5): 833 doi: 10.1016/j.ijrmms.2004.02.001
[12]	Wang G L, Liang Z Y, Zhang L, et al. Study of influence mechanism of Z-type fissure on sandstone strength and fracture behavior. Rock Soil Mech, 2018, 39(Suppl 2): 389 王桂林, 梁再勇, 張亮, 等. Z型裂隙對砂巖強度和破裂行為影響機制研究. 巖土力學, 2018, 39(增刊 2):389
[13]	Afolagboye L O, He J M, Wang S J. Experimental study on cracking behavior of moulded gypsum containing two non-parallel overlapping flaws under uniaxial compression. Acta Mech Sin, 2017, 33(2): 394 doi: 10.1007/s10409-016-0624-9
[14]	Bobet A, Einstein H H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int J Rock Mech Min Sci, 1998, 35(7): 863 doi: 10.1016/S0148-9062(98)00005-9
[15]	Bagde M N, Petro? V. Fatigue and dynamic energy behaviour of rock subjected to cyclical loading. Int J Rock Mech Min Sci, 2009, 46(1): 200 doi: 10.1016/j.ijrmms.2008.05.002
[16]	Chen Y Q, Watanabe K, Kusuda H, et al. Crack growth in Westerly granite during a cyclic loading test. Eng Geol, 2011, 117(3-4): 189 doi: 10.1016/j.enggeo.2010.10.017
[17]	Ghamgosar M, Erarslan N, Williams D J. Experimental investigation of fracture process zone in rocks damaged under cyclic loadings. Exp Mech, 2017, 57(1): 97 doi: 10.1007/s11340-016-0216-4
[18]	Zhu Y B, Huang X, Guo J, et al. Experimental study of fatigue characteristics of gypsum rock under cyclic loading. Chin J Rock Mech Eng, 2017, 36(4): 940 祝艷波, 黃興, 郭杰, 等. 循環荷載作用下石膏質巖的疲勞特性試驗研究. 巖石力學與工程學報, 2017, 36(4):940
[19]	He M M, Chen Y S, Li N, et al. Deformation and energy characteristics of sandstone subjected to uniaxial cyclic loading. J China Coal Soc, 2015, 40(8): 1805 何明明, 陳蘊生, 李寧, 等. 單軸循環荷載作用下砂巖變形特性與能量特征. 煤炭學報, 2015, 40(8):1805
[20]	Ren S, Wang X S, Gao S X, et al. Experimental study on fatigue damage of sandstone based on NMR and acoustic emission. Trans Beijing Inst Technol, 2019, 39(8): 792 任松, 王小書, 高思嫻, 等. 基于NMR和聲發射的砂巖疲勞損傷試驗研究. 北京理工大學學報, 2019, 39(8):792
[21]	Mahabadi O K, Randall N X, Zong Z, et al. A novel approach for micro-scale characterization and modeling of geomaterials incorporating actual material heterogeneity. Geophys Res Lett, 2012, 39(1): L01303
[22]	ündül ?, Amann F, Aysal N, et al. Micro-textural effects on crack initiation and crack propagation of andesitic rocks. Eng Geol, 2015, 193: 267 doi: 10.1016/j.enggeo.2015.04.024
[23]	Ghasemi S, Khamehchiyan M, Taheri A, et al. Crack evolution in damage stress thresholds in different minerals of granite rock. Rock Mech Rock Eng, 2020, 53(3): 1163 doi: 10.1007/s00603-019-01964-9
[24]	Xu J M, Huang D Y, Zhu H C. Relations between macro-and meso-scopic mechanical parameters of granite based on actual distributions of mesocompositions. Chin J Rock Mech Eng, 2016, 35(Suppl 1): 2635 徐金明, 黃大勇, 朱洪昌. 基于細觀組分實際分布的花崗巖宏細觀參數關系. 巖石力學與工程學報, 2016, 35(增刊 1):2635
[25]	Deng S X, Zheng Y L, Feng L P, et al. Application of design of experiments in microscopic parameter calibration for hard rocks of PFC^3D model. Chin J Geotech Eng, 2019, 41(4): 655 鄧樹新, 鄭永來, 馮利坡, 等. 試驗設計法在硬巖PFC^3D模型細觀參數標定中的應用. 巖土工程學報, 2019, 41(4):655
[26]	Shi C, Yang W K, Yang J X, et al. Calibration of micro-scaled mechanical parameters of granite based on a bonded-particle model with 2D particle flow code. Granular Matter, 2019, 21(2): 38 doi: 10.1007/s10035-019-0889-3
[27]	Lu C P, Dou L M, Cao A Y, et al. Research on micro seismic activity rules in deep high-stress concentration district. Chin J Rock Mech Eng, 2008, 27(11): 2303 陸菜平, 竇林名, 曹安業, 等. 深部高應力集中區域礦震活動規律研究. 巖石力學與工程學報, 2008, 27(11):2303
[28]	Xi D Y, Liu X Y, Zhang C Y. Analysis of micro and meso-damage of rock by macro-hysteresis curve. Chin J Rock Mech Eng, 2003, 22(2): 182 doi: 10.3321/j.issn:1000-6915.2003.02.003 席道瑛, 劉小燕, 張程遠. 由宏觀滯回曲線分析巖石的微細觀損傷. 巖石力學與工程學報, 2003, 22(2):182 doi: 10.3321/j.issn:1000-6915.2003.02.003
[29]	Guo Q F, Wu X, Cai M F, et al. Crack initiation mechanism of pre-existing cracked granite. J China Coal Soc, 2019, 44(Suppl 2): 476 郭奇峰, 武旭, 蔡美峰, 等. 預制裂隙花崗巖的裂紋起裂機理試驗研究. 煤炭學報, 2019, 44(增刊 2):476
[30]	Zhu W S, Chen W Z, Shen J. Simulation experiment and fracture mechanism study on propagation of echelon pattern cracks. Chin J Solid Mech, 1998, 19(4): 355 朱維申, 陳衛忠, 申晉. 雁形裂紋擴展的模型試驗及斷裂力學機制研究. 固體力學學報, 1998, 19(4):355
[31]	Li Y P, Wang Y H, Chen L Z, et al. Experimental research on pre-existing cracks in marble under compression. Chin J Geotech Eng, 2004, 26(1): 120 doi: 10.3321/j.issn:1000-4548.2004.01.023 李銀平, 王元漢, 陳龍珠, 等. 含預制裂紋大理巖的壓剪試驗分析. 巖土工程學報, 2004, 26(1):120 doi: 10.3321/j.issn:1000-4548.2004.01.023
[32]	Gao M B, Li T B, Meng L B, et al. The method to identify characteristic stresses of rock in different stages during failure process. Chin J Rock Mech Eng, 2016, 35(Suppl 2): 3577 高美奔, 李天斌, 孟陸波, 等. 巖石變形破壞各階段強度特征值確定方法. 巖石力學與工程學報, 2016, 35(增刊 2):3577