Atomistic simulation of detwinning process and its interaction with self-interstitial atoms in magnesium
-
摘要: 采用分子動力學方法研究了鎂中
$\left\{ {10\bar 12} \right\}$ 拉伸孿晶在剪切載荷下的去孿晶過程，并探討了去孿晶過程中孿晶界面與自間隙原子的交互作用。研究結果表明：去孿晶過程中共格孿晶界對自間隙原子具有吸附作用，自間隙原子被共格孿晶界吸附并隨之遷移，且隨著共格孿晶界的消失而被釋放。通過吸收和釋放這兩種交互作用，去孿晶過程將導致自間隙原子分布更為密集。研究進一步給出了共格孿晶界對自間隙原子的吸附機理，即共格孿晶界存在一個自間隙原子的自發吸收區，0 K下寬度約為0.752 nm，273 K下約為3.59 nm。去孿晶過程與自間隙原子的交互作用也將導致自間隙原子構型的變化。由于自間隙原子的密集分布可在更長時間尺度上誘發位錯環等晶體缺陷，這一研究有助于深入理解鎂及鎂合金的疲勞力學性能。-
關鍵詞:
- 鎂 /
- 分子動力學 /
- $\left\{ {10\bar 12} \right\}$拉伸孿晶 /
- 去孿晶 /
- 自間隙原子
Abstract: Magnesium and its alloys have attracted extensive attention due to their favorable mechanical properties, such as low density and high specific strength. The detwinning process of {$10\bar 12$ } tensile twins subjected to periodic loading is one of the microscopic mechanisms of fatigue damage in magnesium and its alloys. Moreover, self-interstitial atoms (SIAs) widely exist as a typical kind of point defects in metals. The migration, aggregation, and interaction with other defects, of SIAs affect the metal mechanical properties. In this work, molecular dynamics simulation was employed to study the detwinning process of {$10\bar 12$ } twins under shear loads in magnesium, focusing on the interaction between the twin boundary and SIAs in the detwinning process. A simulation system containing two coherent twin boundaries (CTBs) with periodic boundary conditions applied along the two in-plane directions was adopted. The classic embedded atom method (EAM) interatomic potential developed by Liu et. al was used for simulation accuracy and comparison with other studies. The simulation results show that the SIAs are absorbed by the CTBs and migrate along with them. The absorbed SIAs can be released with the disappearance of the CTBs during the detwinning process. By the SIA adsorption and release, detwinning process will result in a more concentrated SIA distribution. The simulation results reveal that SIAs will be adsorbed by CTB if the distance between the CTB and SIA is less than 0.752 nm at 0 K and 3.59 nm at 273 K. The energy barrier of the adsorption process is also obtained using the nudged elastic band (NEB) method. The SIA spatial distribution changes after the SIA interactions with CTB in detwinning process. Given that the crystal defects such as dislocation loops can be induced by the dense distribution of SIAs at a long timescale, this study clarifies the fatigue mechanical properties of magnesium and magnesium alloys subjected to periodic loading.-
Key words:
- magnesium /
- molecular dynamics /
- {$10\bar 12$} twin /
- detwinning /
- self-interstitial atoms
-
圖 1 模型示意圖（圖中孿晶界處原子與間隙原子均被放大顯示，黑色虛折線標識了孿晶內外的基平面）
Figure 1. Schematic of simulation model (Atoms at the coherent twin boundaries (CTBs) and the self-interstitial atoms (SIAs) are magnified for observation. The black dotted lines denote the basal planes inside and outside the twin)
圖 2 密排六方金屬中可能存在的8種間隙構型示意圖（a）及本文分子動力學模擬中存在的間隙構型（b）
Figure 2. Schematic of eight possible configurations of SIAs in hcp metals (a) and configurations obtained in this work (b)
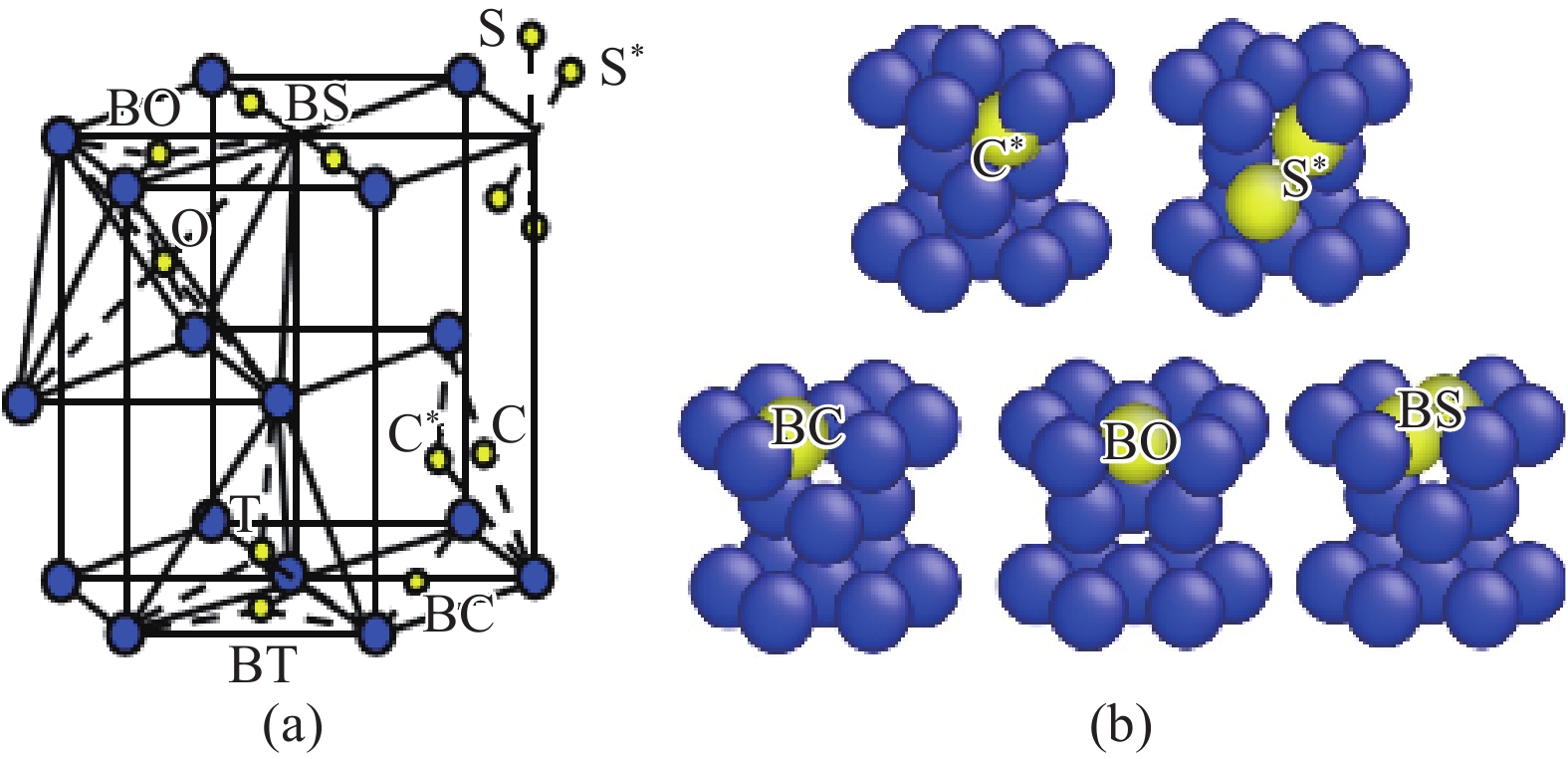
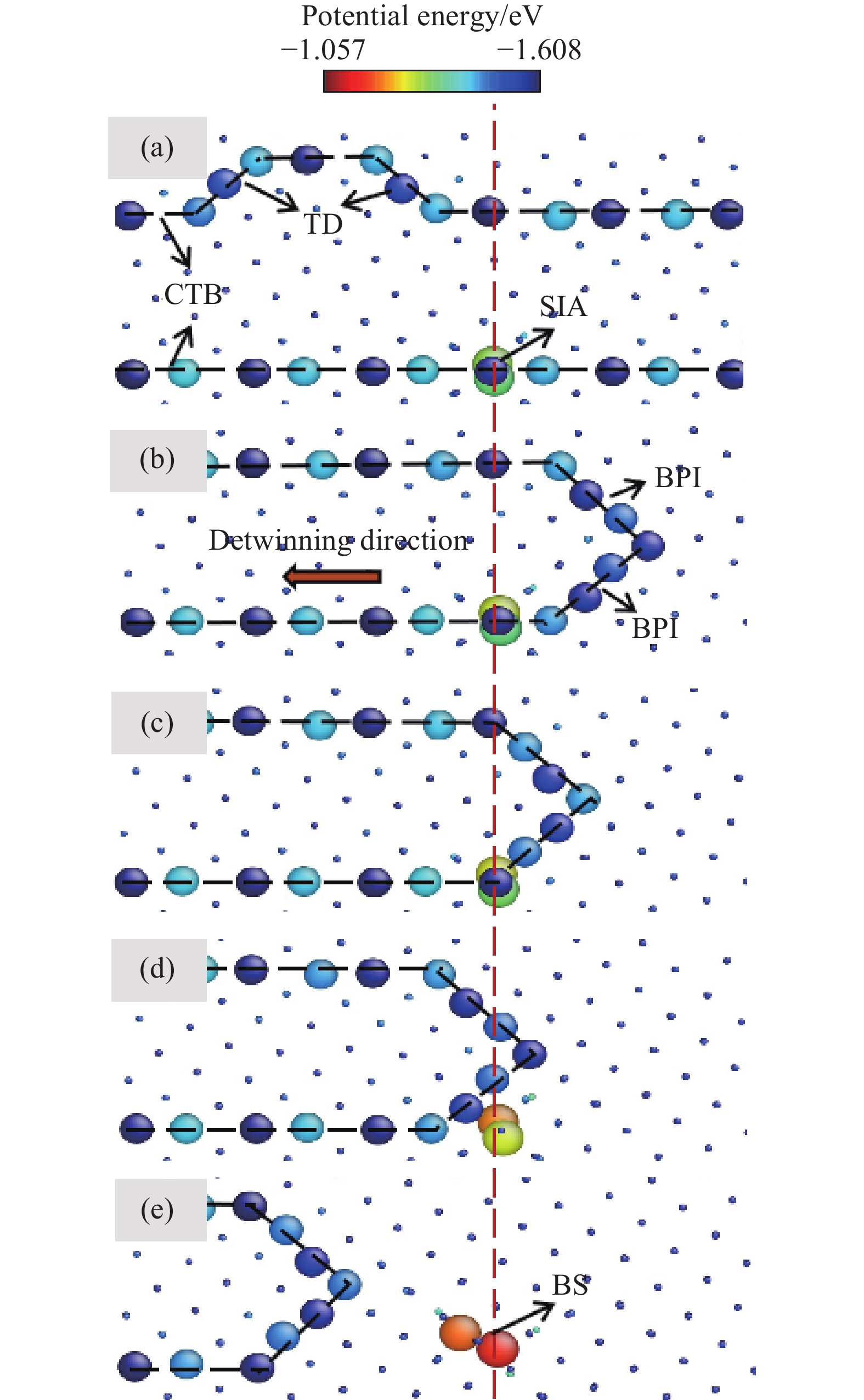
圖 3 去孿晶過程（a）及去孿晶過程與自間隙原子交互作用（b）（圖中的虛線所示為孿晶內外兩部分晶體各自的基面。原子按其勢能大小著色。晶界處原子與間隙原子均被放大顯示，以便觀察）
Figure 3. Detwinning process (a) and interaction between the CTBs and the SIAs (b) (The dotted lines denote the basal planes inside and outside the twin. Atoms are colored according to potential energy. Atoms on the CTB and in the interstitial structure are magnified for observation)
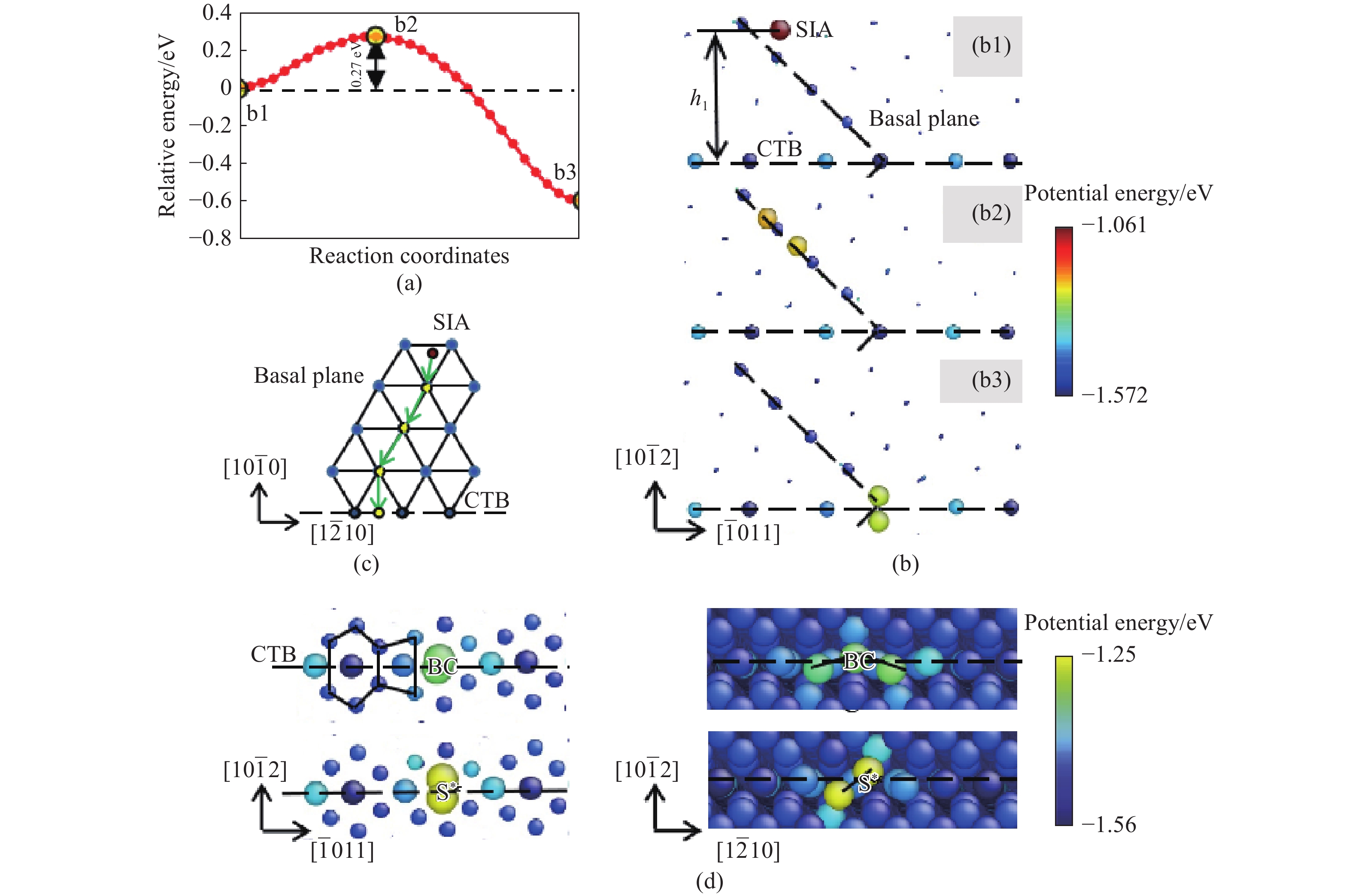
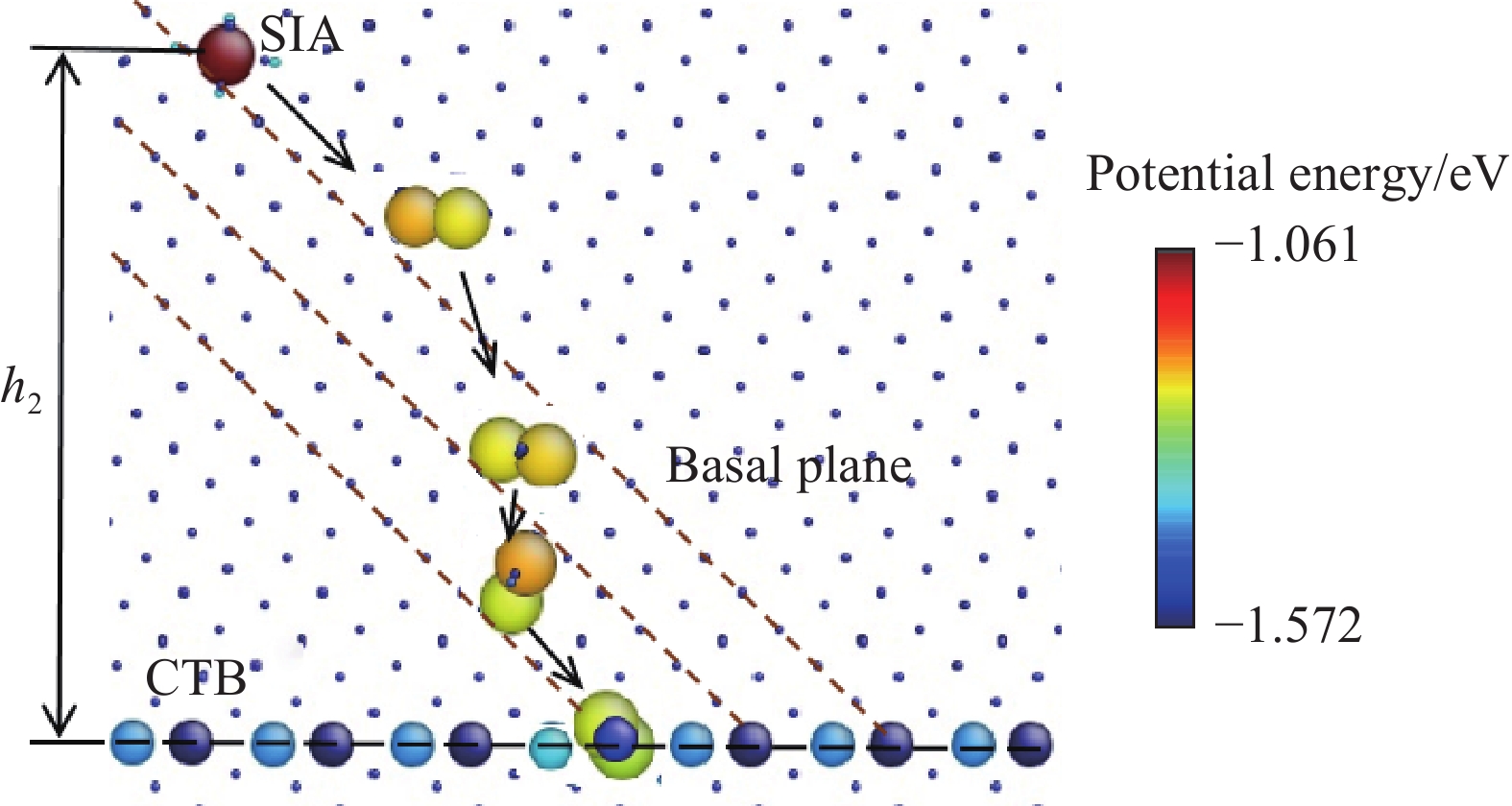
圖 4 NEB計算的系統勢能形貌（a）；0 K時自間隙原子位于自發吸收區內被共格孿晶界吸收的過程（b）（原子按其勢能大小著色，孿晶界處原子與間隙原子均被放大顯示）；從[0001]方向觀察吸收的路徑（c）；從
$\left[ {1\bar 210} \right]$ 及$\left[ {\bar 1011} \right]$ 兩個方向上觀察被共格孿晶界吸收后間隙原子的構型（d）（原子按其勢能大小著色，左圖晶界處原子與間隙原子均被放大顯示，以便觀察）Figure 4. Potential energy landscape (a) associated with the atomic configurations described in (b); Process of SIA absorption by CTB in the spontaneous absorption region at 0 K (b) (Atoms are colored according to potential energy. Atoms on the CTB and in the interstitial structure are magnified for observation); Path of absorption observed in the [0001] direction (c); Configurations of SIAs absorbed by the CTB observed in the directions of
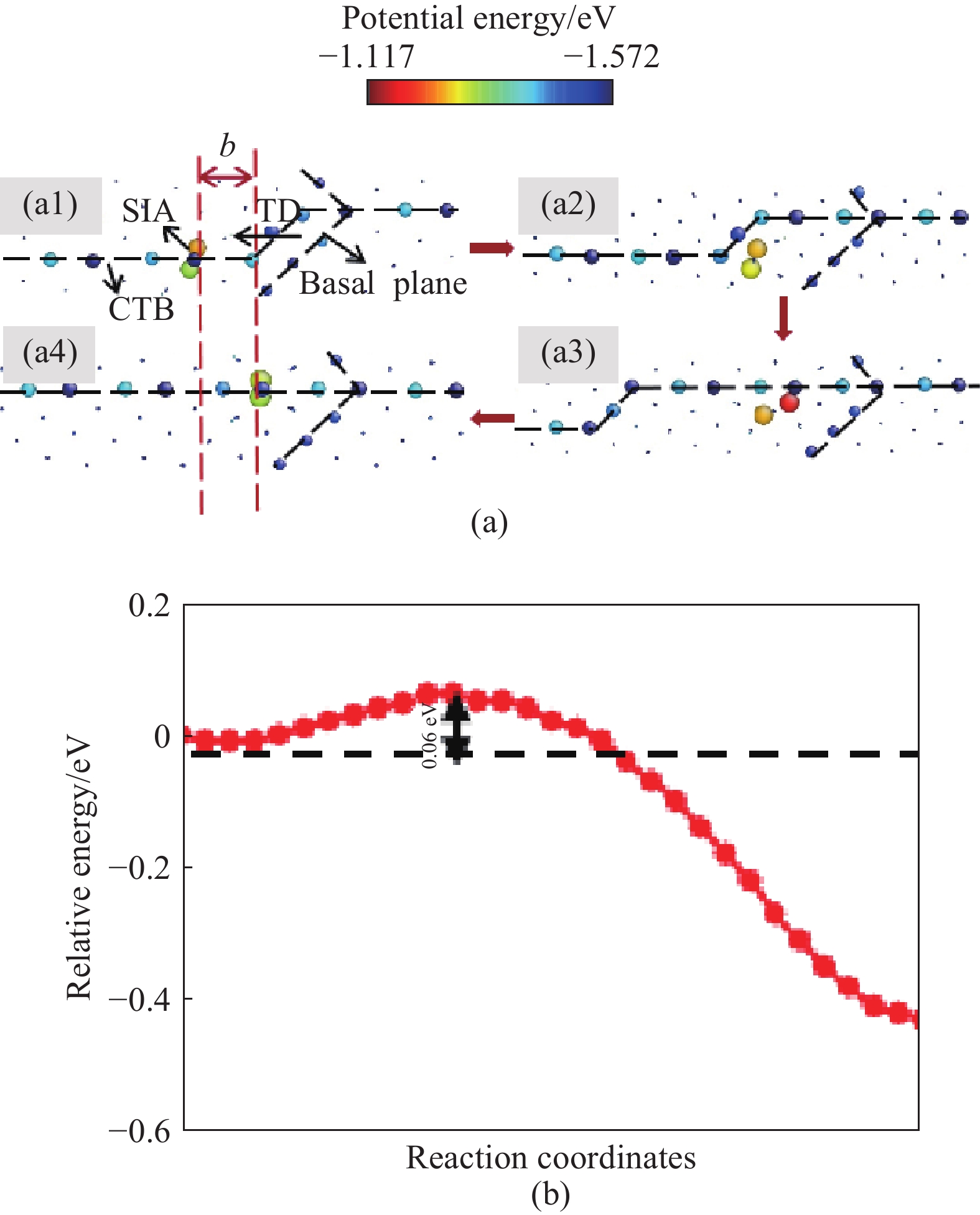
$\left[ {1\bar 210} \right]$ and$\left[ {\bar 1011} \right]$ (d) (Atoms are colored according to potential energy. Atoms on the CTB and in the interstitial structure are magnified for observation in the left part)
圖 5 273 K時自間隙原子位于自發吸收區內被共格孿晶界吸收的過程（原子按其勢能大小著色，孿晶界處原子與間隙原子均被放大顯示）
Figure 5. Process of SIA absorption by a CTB in the spontaneous absorption region at 273 K (Atoms are colored according to potential energy. Atoms on the CTB and in the interstitial structure are magnified for observation)
圖 6 0 K孿晶位錯與共格孿晶界上自間隙原子的交互作用（a）（原子按其勢能大小著色。晶界、用于參照的基平面，以及間隙結構中的原子均被放大顯示，以便觀察），及NEB計算的系統勢能形貌（b）
Figure 6. Interaction of TDs and SIAs (a) (Atoms are colored according to potential energy. The atoms in twin boundary, basal planes for reference and in the interstitial structure are magnified for observation), potential energy landscape (b) associated with the atomic configurations described in (a)
圖 7 自間隙原子被共格孿晶界釋放的過程（晶界及間隙結構中的原子均被放大顯示）
Figure 7. Release of SIAs by the CTB (Atoms on the CTB and in the interstitial structure are magnified)
259luxu-164<th id="5nh9l"></th> <strike id="5nh9l"></strike> <th id="5nh9l"><noframes id="5nh9l"><th id="5nh9l"></th> <strike id="5nh9l"></strike> <th id="5nh9l"><noframes id="5nh9l"> <th id="5nh9l"></th> <strike id="5nh9l"><noframes id="5nh9l"><span id="5nh9l"></span> <span id="5nh9l"><noframes id="5nh9l"><span id="5nh9l"></span> <strike id="5nh9l"><noframes id="5nh9l"><strike id="5nh9l"></strike> <span id="5nh9l"><noframes id="5nh9l"> <span id="5nh9l"><noframes id="5nh9l"> <span id="5nh9l"></span> <span id="5nh9l"><video id="5nh9l"></video></span> <th id="5nh9l"><noframes id="5nh9l"><th id="5nh9l"></th> -
參考文獻
[1] Yu Q, Qi L, Chen K, et al. The nanostructured origin of deformation twinning. Nano Lett, 2012, 12(2): 887 doi: 10.1021/nl203937t [2] Kelley E W, Hosford W F. Plane-strain compression of magnesium and magnesium alloy crystals. Trans Metall Soc AIME, 1968, 242(1): 5 [3] Guo Y F, Xu S, Tang X Z, er al. Twinnability of hcp metals at the nanoscale. J Appl Phys, 2014, 115(22): 224902 doi: 10.1063/1.4881756 [4] Meng Q, Cai Q W, Jiang H T, et al. {0002} double peak texture of AZ31 magnesium alloy during uniaxial tension. Chin J Rare Met, 2011, 35(2): 159 doi: 10.3969/j.issn.0258-7076.2011.02.001孟強, 蔡慶伍, 江海濤, 等. AZ31鎂合金單軸拉伸過程中的{0002}雙峰織構觀察. 稀有金屬, 2011, 35(2):159 doi: 10.3969/j.issn.0258-7076.2011.02.001 [5] Wang Y N, Huang J C. The role of twinning and untwinning in yielding behavior in hot-extruded Mg?Al?Zn alloy. Acta Mater, 2007, 55(3): 897 doi: 10.1016/j.actamat.2006.09.010 [6] Yin S M, Yang F, Yang X M, et al. The role of twinning–detwinning on fatigue fracture morphology of Mg?3%Al?1%Zn alloy. Mater Sci Eng A, 2008, 494(1-2): 397 doi: 10.1016/j.msea.2008.04.056 [7] Zhang Y, Liu T M, Xu S, et al. Detwinning behavior of an extruded AZ31 magnesium alloy during uniaxial compression. Trans Mater Heat Treat, 2013, 34(8): 26張愔, 劉天模, 徐舜, 等. 擠壓態AZ31鎂合金單向壓縮過程中的退孿生行為. 材料熱處理學報, 2013, 34(8):26 [8] Sarker D, Chen D L. Detwinning and strain hardening of an extruded magnesium alloy during compression. Scripta Mater, 2012, 67(2): 165 doi: 10.1016/j.scriptamat.2012.04.007 [9] Morrow B M, McCabe R J, Cerreta E K, et al. In-situ TEM observation of twinning and detwinning during cyclic loading in Mg. Metall Mater Trans A, 2014, 45(1): 36 doi: 10.1007/s11661-013-1765-0 [10] Sun Q, Xia T, Tan L, et al. Influence of { $$ } twin characteristics on detwinning in Mg?3Al?1Zn alloy. Mater Sci Eng A, 2018, 735: 243 doi: 10.1016/j.msea.2018.08.051[11] Lou C, Zhang X Y, Wang R H, et al. Effects of untwinning and { $$ } twin lamellar structure on the mechanical properties of Mg alloy. Acta Metall Sin, 2013, 49(3): 291 doi: 10.3724/SP.J.1037.2012.00582婁超, 張喜燕, 汪潤紅, 等. 退孿生行為以及{$$ }孿晶片層結構對鎂合金力學性能的影響. 金屬學報, 2013, 49(3):291 doi: 10.3724/SP.J.1037.2012.00582[12] Mendelev M I, King A H. The interactions of self-interstitials with twin boundaries. Philos Mag, 2013, 93(10-12): 1268 doi: 10.1080/14786435.2012.747012 [13] Yu W S, Shen S P. Energetics of point defect interacting with grain boundaries undergone plastic deformations. Int J Plast, 2016, 85: 93 doi: 10.1016/j.ijplas.2016.07.004 [14] Li X T, Tang X Z, Guo Y F. Minimum energy path of a solute atom diffusing to an edge dislocation core in Al-Mg alloys based on empirical atomic potential. Chin J Eng, 2019, 41(7): 898李曉彤, 湯笑之, 郭雅芳. 經驗原子勢下鋁鎂合金中溶質原子向位錯芯遷移的最低能量路徑. 工程科學學報, 2019, 41(7):898 [15] Hood G M. Point defect diffusion in α-Zr. J Nucl Mater, 1988, 159: 149 doi: 10.1016/0022-3115(88)90091-8 [16] Peng Q, Ji W, Huang H C, et al. Stability of self-interstitial atoms in hcp-Zr. J Nucl Mater, 2012, 429(1-3): 233 doi: 10.1016/j.jnucmat.2012.06.010 [17] Samolyuk G D, Barashev A V, Golubov S I, et al. Analysis of the anisotropy of point defect diffusion in hcp Zr. Acta Mater, 2014, 78: 173 doi: 10.1016/j.actamat.2014.06.024 [18] Serra A, Bacon D J, Osetsky Y N. Strengthening and microstructure modification associated with moving twin boundaries in hcp metals. Philos Mag Lett, 2007, 87(7): 451 doi: 10.1080/09500830701244812 [19] Deng Y F, Wang Y X, He Y, et al. Atomic simulation of defect behavior in metal zirconium. J Shengyang Normal Univ Nat Sci Ed, 2018, 36(4): 295鄧玉福, 王鈺鑫, 何燕, 等. 原子模擬金屬鋯中點缺陷行為. 沈陽師范大學學報(自然科學版), 2018, 36(4):295 [20] Hatami F, Feghhi S A H, Arjhangmehr A, et al. Interaction of primary cascades with different atomic grain boundaries in α-Zr: An atomic scale study. J Nucl Mater, 2016, 480: 362 doi: 10.1016/j.jnucmat.2016.05.036 [21] Pasianot R C. Self-interstitials structure in the hcp metals: A further perspective from first-principles calculations. J Nucl Mater, 2016, 481: 147 doi: 10.1016/j.jnucmat.2016.09.021 [22] Monti A M, Sarce A, Grande N S D, et al. Point defects and sink strength in h. c. p. metals. Philos Mag A, 1991, 63(5): 925 doi: 10.1080/01418619108213925 [23] de Diego N, Bacon D J. A computer simulation study of interstitial-twin boundary interactions in h. c. p. metals. Modell Simul Mater Sci Eng, 1995, 3(6): 797 doi: 10.1088/0965-0393/3/6/004 [24] Liu X Y, Ohotnicky P P, Adams J B, et al. Anisotropic surface segregation in Al-Mg alloys. Surf Sci, 1997, 373(2-3): 357 doi: 10.1016/S0039-6028(96)01154-5 [25] Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys, 1995, 117(1): 1 doi: 10.1006/jcph.1995.1039 [26] Li J. AtomEye: an efficient atomistic configuration viewer. Modell Simul Mater Sci Eng, 2003, 11(2): 173 doi: 10.1088/0965-0393/11/2/305 [27] Tang X Z, Zu Q, Guo Y F. The diffusive character of extension twin boundary migration in magnesium. Mater, 2018, 2: 208 [28] Luque A, Ghazisaeidi M, Curtin W A. A new mechanism for twin growth in Mg alloys. Acta Mater, 2014, 81: 442 doi: 10.1016/j.actamat.2014.08.052 [29] Gleiter H. The mechanism of grain boundary migration. Acta Metall, 1969, 17(5): 565 doi: 10.1016/0001-6160(69)90115-1 [30] Gong M Y, Hirth J P, Liu Y, et al. Interface structures and twinning mechanisms of { $$ } twins in hexagonal metals. Mater Res Lett, 2017, 5(7): 449 doi: 10.1080/21663831.2017.1336496[31] Bacon D J. A review of computer models of point defects in hcp metals. J Nucl Mater, 1988, 159: 176. -
下載:
點擊查看大圖
計量
- 文章訪問數: 2169
- HTML全文瀏覽量: 910
- PDF下載量: 70
- 被引次數: 0
