Nonsmooth active control method for base-smart isolated structures with roller bearings
-
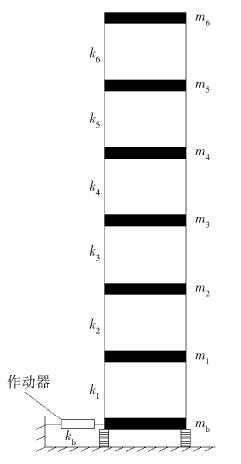
摘要: 以滾軸支座基礎隔震結構作為受控結構研究對象, 在該隔震結構的隔震層施加主動控制裝置, 形成智能隔震體系, 以控制隔震層的位移, 提高結構的安全性. 在智能隔震結構中引入非光滑控制算法, 基于隔震層位移和速度反饋, 提出了智能隔震結構的非光滑控制算法, 進一步根據Lyapunov穩定理論, 推導了在非光滑控制下智能控制閉環系統的全局有限時間穩定性. 結合一棟六層滾軸支座基礎隔震結構, 進行了非光滑主動控制算法下和LQG主動控制算法下的地震響應控制仿真分析. 結果表明, 智能隔震結構可有效控制結構的位移, 與被動隔震結構相比較上部結構的地震響應有一定程度的減小, 同時提出的非光滑控制算法與LQG控制算法相比較具有更好的控制效果, 相比LQG控制算法通過較少的反饋量即可實現反饋控制, 且非光滑控制算法具有良好的穩定性.Abstract: In applied structural control technology, base-isolated technology has become popular due to its advantage of simple shock absorption, stable performance, and reasonable cost. Currently, base isolation is extensively applied worldwide, and its role in mitigating the seismic response of structures continues to grow. Moreover, it has been proven effective in decreasing seismic response of structures under recent strong earthquakes. However, the displacement at the isolation layer is sometimes large under strong earthquakes, which will decrease the safety of the structure and perhaps lead to the failure of the isolation layer. Therefore, in this study, the base-isolated structure with roller bearings is taken to investigate the seismic response control of structures, and the active control devices are added in the isolation layer of the isolated structure to decrease the seismic displacement at the isolation layer, so that a smart-isolated structure is formed. Nonsmooth control algorithm is introduced in the smart-isolated structure. Based on the feedback of the velocity and displacement of the isolation layer, nonsmooth control algorithm is proposed for designing the smart-isolated structure. Moreover, according to Lyapunov stable theory, the global finite time stability of intelligent control closed-loop system under nonsmooth control is deduced. A six-layer isolated structure with roller bearings is used as an example, and a simulation analysis of seismic response control is performed based on the nonsmooth active control algorithm and linear quadratic Gaussian (LQG) active control algorithm. The results show that the smart-isolated technology can effectively control seismic displacement at the isolation layer, and compared with the passive isolated technology, the superstructure seismic response is significantly decreased. Meanwhile, the results demonstrate that compared with the LQG control algorithm, the nonsmooth control algorithm has a better control effect and can implement feedback control for base-isolated structures by using fewer feedbacks. Furthermore, the nonsmooth control algorithm has great stability.
-
圖 2 滾軸支座單元和滾動示意圖. (a) 滾軸支座單元; (b) 滾軸支座滾動
Figure 2. Unit and roll of roller bearing: (a) unit of roller bearing; (b) roll of roller bearing
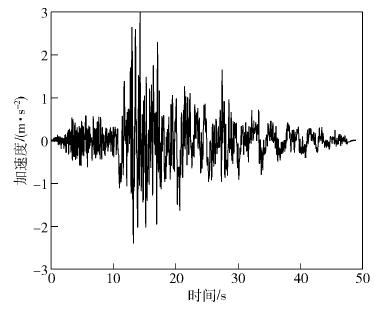
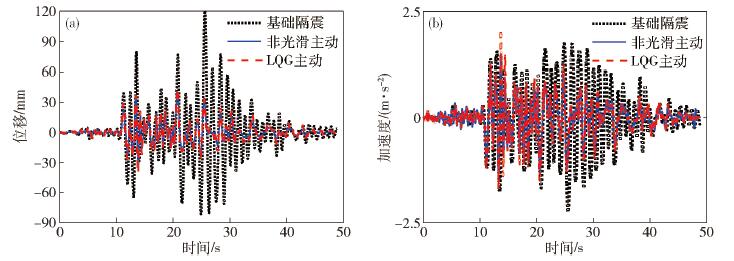
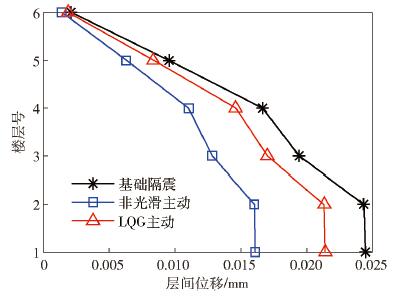
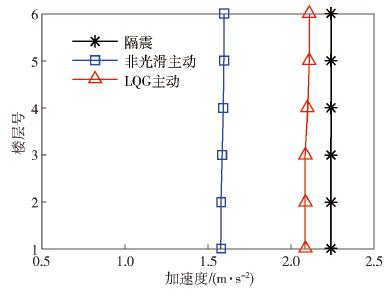
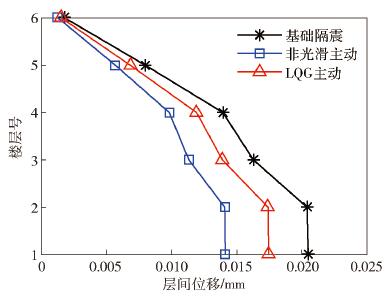
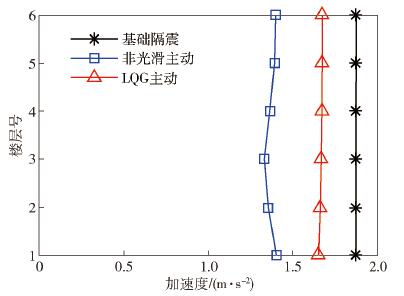
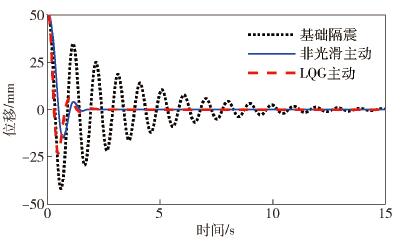
圖 11 LK0676波作用下結構隔震層響應曲線對比. (a) LK0676波作用下隔震層位移曲線對比; (b) LK0676波作用下隔震層加速度曲線對比
Figure 11. Curve comparison of structural isolation layer response under LK0676 wave: (a) curve comparison of isolation layer displacement under LK0676 wave; (b) curve comparison of isolation layer acceleration under LK0676 wave
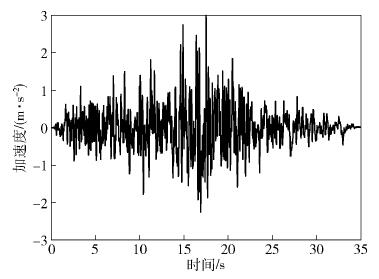
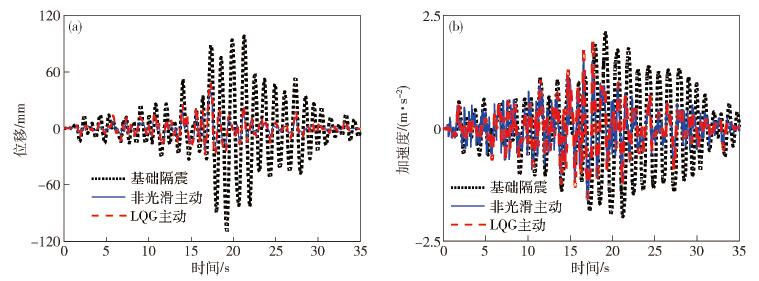
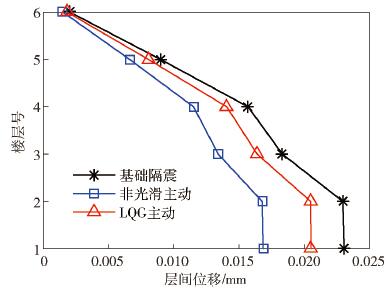
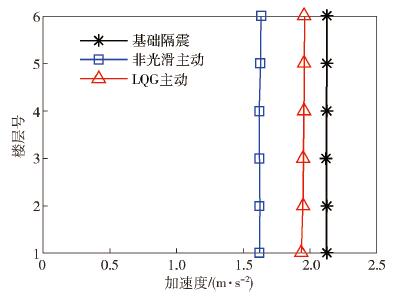
圖 12 LK0714波作用下結構隔震層響應曲線對比. (a) LK0714波作用下隔震層位移曲線對比; (b) LK0714波作用下隔震層加速度曲線對比
Figure 12. Curve comparison of structural isolation layer response under LK714 wave: (a) curve comparison of isolation layer displacement under LK714 wave; (b) curve comparison of isolation layer acceleration under LK714 wave
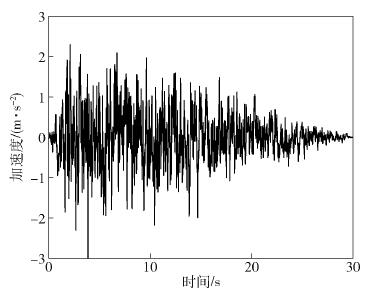
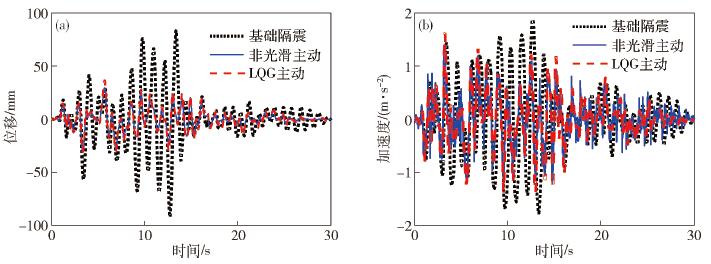
圖 13 人工波作用下結構隔震層響應曲線對比. (a) 人工波作用下隔震層位移曲線對比; (b) 人工波作用下隔震層加速度曲線
Figure 13. Curve comparison of structural isolation layer response under artificial wave: (a) curve comparison of isolation layer displacement under artificial wave; (b) curve comparison of isolation layer acceleration under artificial wave
圖 14 LK0676波作用下上部結構層間位移峰值
Figure 14. Inter-story displacement peak of superstructure under LK0676
圖 16 LK0714波作用下上部結構層間位移峰值
Figure 16. Inter-story displacement peak of superstructure under LK0714
圖 18 人工波作用下上部結構層間位移峰值
Figure 18. Inter-story displacement peak of superstructure under artificial wave
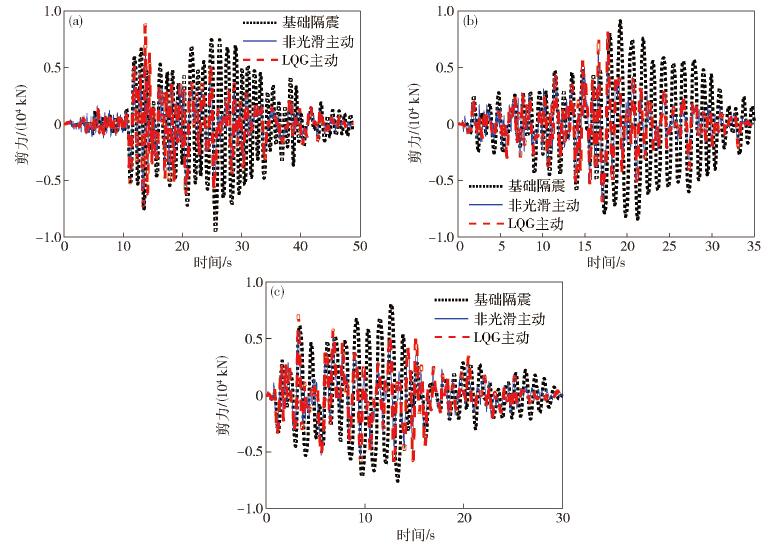
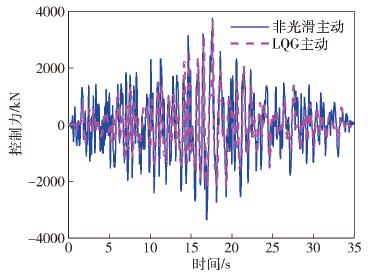
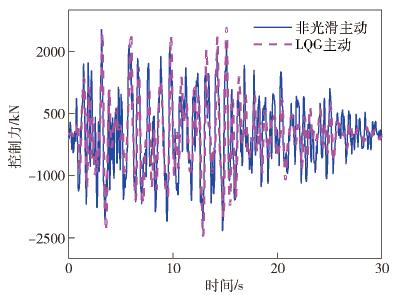
圖 20 三種波作用下結構隔震層底部剪力曲線. (a) LK0676波作用下結構隔震層底部剪力曲線; (b) LK0714波作用下結構隔震層底部剪力曲線; (c) 人工波作用下結構隔震層底部剪力曲線
Figure 20. Bottom shear force of structural isolation layer under three waves: (a) bottom shear force of structural isolation layer under; (b) bottom shear force of structural isolation layer under LK0714 wave; (c) bottom shear force of structural isolation layer under artificial wave
圖 24 基礎隔震結構和智能隔震結構復位曲線
Figure 24. Reset curve of base-isolated structure and smart-isolated structure
表 1 MATLAB模型與ETABS模型周期
Table 1. Period of MATLAB model and ETABS model
振型號 MTALB周期/s ETABS周期/s 1 1.160 1.209 2 0.436 0.422 3 0.275 0.235 4 0.218 0.182 5 0.187 0.142 6 0.180 0.116 
下載: 導出CSV
表 2 三條波分別作用下的隔震層響應峰值
Table 2. Peak values of isolation layer responses under three different waves
控制策略 LK0676波 LK0714 人工波 位移/
mm速度/
(m·s-1)加速度/
(m·s-2)位移/
mm速度/
(m·s-1)加速度/
(m·s-2)位移/
mm速度/
(m·s-1)加速度/
(m·s-2)隔震 120.65 0.49 2.24 110.58 0.54 2.12 91.92 0.49 1.87 LQG 43.57 0.37 2.06 48.92 0.36 1.93 36.48 0.24 1.63 非光滑 40.10 0.32 1.48 39.56 0.27 1.59 29.44 0.21 1.25
下載: 導出CSV
表 3 隔震層底部剪力峰值
Table 3. Peak value of bottom shear force in the isolation layer
控制策略 剪力峰值/(103 kN) LK0676波 LK0714波 人工波 隔震 9.602 9.098 8.029 LQG 8.910 8.317 7.107 非光滑 6.678 6.903 5.672
下載: 導出CSV
259luxu-164<th id="5nh9l"></th> <strike id="5nh9l"></strike> <th id="5nh9l"><noframes id="5nh9l"><th id="5nh9l"></th> <strike id="5nh9l"></strike> <th id="5nh9l"><noframes id="5nh9l"> <th id="5nh9l"></th> <strike id="5nh9l"><noframes id="5nh9l"><span id="5nh9l"></span> <span id="5nh9l"><noframes id="5nh9l"><span id="5nh9l"></span> <strike id="5nh9l"><noframes id="5nh9l"><strike id="5nh9l"></strike> <span id="5nh9l"><noframes id="5nh9l"> <span id="5nh9l"><noframes id="5nh9l"> <span id="5nh9l"></span> <span id="5nh9l"><video id="5nh9l"></video></span> <th id="5nh9l"><noframes id="5nh9l"><th id="5nh9l"></th> -
參考文獻
[1] Zhou F L. Seismic Control in Engineering Structures. Beijing: Seismological Press, 1997周福霖. 工程結構減震控制. 北京: 地震出版社, 1997 [2] Ou J P. Structural Vibration Control-Active, Semi-active and Intelligent control. Beijing: Science Press, 2003歐進萍. 結構振動控制: 主動、半主動和智能控制. 北京: 科學出版社, 2003 [3] Wang J W, Yang Y F, Qian Y H. Design of controller for torsion vibration device based on pole assignment method. Exp Technol Manage, 2014, 31(7): 86 https://www.cnki.com.cn/Article/CJFDTOTAL-SYJL201407025.htm王佳偉, 楊亞非, 錢玉恒. 基于極點配置方法的扭轉振動裝置控制器設計. 實驗技術與管理, 2014, 31(7): 86 https://www.cnki.com.cn/Article/CJFDTOTAL-SYJL201407025.htm [4] Tong S W, Tang H P. Research on approximate discrete instantaneous optimal control algorithm and optimization of the actuator positions. J Vib Eng, 2016, 29(5): 920 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC201605021.htm童少偉, 唐懷平. 近似離散瞬時最優控制及作動器位置優化研究. 振動工程學報, 2016, 29(5): 920 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC201605021.htm [5] Yang J N, Wu J C, Kawashima K, et al. Hybrid control of seismic-excited bridge structure. Earthquake Eng Struct Dyn, 1995, 24(11): 1437 doi: 10.1002/eqe.4290241103 [6] Yang J N, Wu J C, Agrawal A K. Sliding mode control for seismically excited linear structures. J Eng Mech, 1995, 121(12): 1386 doi: 10.1061/(ASCE)0733-9399(1995)121:12(1386) [7] Rosier L. Homogeneous Lyapunov function for homogeneous continuous vector field. Syst Control Lett, 1992, 19(6): 467 doi: 10.1016/0167-6911(92)90078-7 [8] Kawski M. Stability and nilpotent approximations//Proceedings of the 27th IEEE Conference on Decision and Control. Austin, 1988: 1244 [9] Hermes H. Asymptotically stabilizing feedback controls. J Differential Equations l, 1991, 92(1): 76 doi: 10.1016/0022-0396(91)90064-G [10] Wang S. Study on Non-smooth Control Algorithm for Smart Base Isolated Benchmark Building[Dissertation]. Guangzhou: Guangzhou University, 2016王思. 基于Benchmark智能隔震結構的非光滑控制算法的研究與分析[學位論文]. 廣州: 廣州大學, 2016 [11] Ma K M. Design of continuous non-smooth attitude control laws for spacecraft. J Astronautics, 2012, 33(6): 713 doi: 10.3873/j.issn.1000-1328.2012.06.005馬克茂. 航天器連續非光滑姿態控制律設計. 宇航學報, 2012, 33(6): 713 doi: 10.3873/j.issn.1000-1328.2012.06.005 [12] Ma K M. Non-smooth design and implementation of high-precision guidance laws. J Ball, 2013, 25(2): 1 https://www.cnki.com.cn/Article/CJFDTOTAL-DDXB201302003.htm馬克茂. 高精度制導律的非光滑設計與實現. 彈道學報, 2013, 25(2): 1 https://www.cnki.com.cn/Article/CJFDTOTAL-DDXB201302003.htm [13] Wang J H, Wang Q, Ma K M. Non-smooth controller design for permanent magnet synchronous motors. Comput Simul, 2016, 33(3): 227 https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201603050.htm王建暉, 王清, 馬克茂. 一種永磁同步電機非光滑控制器設計. 計算機仿真, 2016, 33(3): 227 https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201603050.htm [14] Li S H, Ding S H, Du H B, et al. Theory and Application of Non-smooth Control. Beijing: Science Press, 2013李世華, 丁世宏, 都海波, 等. 非光滑控制理論與應用. 北京: 科學出版社, 2013 [15] Li H N, Li Z X, Qi A, et al. Structure Vibration and Control. Beijing: China Architecture & Building Press, 2005李宏男, 李忠獻, 祈皚, 等. 結構振動與控制. 北京: 中國建筑工業出版社, 2005 [16] Jiang H B, Li C X, Ma S D, et al. Path tracking control of automatic parking for intelligent vehicle based on non-smooth control strategy. J Jiangsu Univ Nat Sci Ed, 2017, 38(5): 497 https://www.cnki.com.cn/Article/CJFDTOTAL-JSLG201705001.htm江浩斌, 李臣旭, 馬世典, 等. 智能車輛自動泊車路徑跟蹤的非光滑控制策略. 江蘇大學學報: 自然科學版, 2017, 38(5): 497 https://www.cnki.com.cn/Article/CJFDTOTAL-JSLG201705001.htm [17] Yang C. Research on Buck Type DC-DC Converter Control System Based on Finite-time Control Technique[Dissertation]. Hefei: Hefei University of Technology, 2017楊晨. 基于有限時間控制技術的Buck型DC-DC變換器控制系統研究[學位論文]. 合肥: 合肥工業大學, 2017 [18] Wang Q, Wang J H, Ma K M, et al. Nonsmooth control algorithm for structural vibration control and its applications. Earthquake Eng Eng Dyn, 2016, 36(5): 207 https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201605025.htm王清, 王建暉, 馬克茂, 等. 結構振動控制的非光滑控制算法及其應用. 地震工程與工程振動, 2016, 36(5): 207 https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201605025.htm [19] Ma K M. Design of non-smooth guidance law with terminal line-of-sight constraint. J Ball, 2011, 23(2): 14 https://www.cnki.com.cn/Article/CJFDTOTAL-DDXB201102005.htm馬克茂. 帶有終端視線約束的非光滑制導律設計. 彈道學報, 2011, 23(2): 14 https://www.cnki.com.cn/Article/CJFDTOTAL-DDXB201102005.htm -
點擊查看大圖
計量
- 文章訪問數: 629
- HTML全文瀏覽量: 415
- PDF下載量: 14
- 被引次數: 0
