考慮樓板效應的外環板式梁柱節點抗彎承載力

王玲玲; 牟犇; 林旭川; 河野昭彥

doi:10.13374/j.issn2095-9389.2019.06.015

考慮樓板效應的外環板式梁柱節點抗彎承載力

doi: 10.13374/j.issn2095-9389.2019.06.015

1.
青島理工大學土木工程學院, 青島 266033
2.
中國地震局工程力學研究所, 哈爾濱 150080
3.
九州大學人間環境學府, 福岡 8120053

基金項目:

國家重點研發計劃資助項目 2017YFC1500605

國家自然科學基金資助項目 51678542

中國博士后面上資助項目 2017M612226

詳細信息

通訊作者:
牟犇, E-mail: mouben98@163.com

中圖分類號: TU392.3
計量
- 文章訪問數: 981
- HTML全文瀏覽量: 415
- PDF下載量: 26
- 被引次數: 0
出版歷程
- 收稿日期: 2018-05-16
- 刊出日期: 2019-06-01

Flexural capacity of beam-to-column joints with external diaphragm considering the slab effect

1.
Department of Civil Engineering, Qingdao University of Technology, Qingdao 266033, China
2.
Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
3.
Graduate School of Human-Environment Studies, Kyushu University, Fukuoka 8120053, Japan

More Information

Corresponding author: MOU Ben, E-mail: mouben98@163.com

摘要

摘要: 樓板的存在對梁柱節點的局部受力影響顯著, 在梁柱節點設計中, 若僅僅把樓板與鋼梁的組合效應作為安全儲備, 可能會產生結構由"強柱弱梁"轉變成"強梁弱柱"的顛覆性結果, 因此忽略混凝土樓板對節點承載力及剛度的影響是造成破壞的重要原因.基于已完成的帶樓板的T型梁柱節點低周往復荷載試驗, 建立了非線性有限元分析模型.為了更加全面地了解鋼梁-樓板組合節點的工作機制, 進一步補充完善試驗研究的不足, 模型考慮了樓板與鋼梁之間的栓釘連接以及材料非線性等因素, 模型的計算結果與試驗結果具有高吻合度.在此基礎上, 通過有限元參數分析, 詳細分析了構件尺寸效應、軸壓比、樓板厚度、樓板強度和柱寬厚比共五個參數對考慮樓板影響的外環板式梁柱節點抗震性能的影響.結果表明尺寸效應、軸壓比對梁端抗彎承載力及剛度的影響小到可以忽略, 樓板厚度、樓板強度和柱寬厚比對梁端抗彎承載力有顯著影響.結合理論分析進一步提出了考慮樓板影響的外環板式梁柱節點梁端抗彎承載力計算公式, 通過對比公式計算結果與試驗、有限元分析結果可得, 該計算公式可較好的計算帶樓板外環板式梁柱節點梁端抗彎承載力.
- 樓板效應 /
- 外環板 /
- 梁柱節點 /
- 組合結構 /
- 非線性有限元分析
Abstract: The existence of concrete slab has significant influence on the local mechanical characteristic of the beam-to-column joint. In the design of beam-to-column joints, if the composite effects of steel beam and concrete slab are considered particularly as safety stock, the counteractive result of "strong column and weak beam" or "strong beam and weak column" may be produced; therefore, ignoring the influence of concrete slab affect the bearing capacity and stiffness of the joints. Based on the results of a full-scale cyclic test conducted on T-shaped beam-to-column joints, a detailed nonlinear finite element model was proposed. To completely understand the working mechanism of composite joints and further improve the experimental research, the nonlinear material properties and the shear effect of the connectors between concrete slab and steel beam were considered in the model. The results from the model agree well with the test results. Moreover, an extensive parametric study was performed to examine the seismic behavior of the joints. Parameters, such as the size effect, axial-load ratio, slab thickness, concrete compressive strength, and diameter-to-thickness ratio of the column, were investigated. The results show that the size and axial-load ratio have insignificant effect on the flexural capacity and stiffness of beam end, whereas the slab thickness, concrete compressive strength and diameter-to-thickness ratio of the column have significant effect on it. Furthermore, a calculation formula of flexural capacity was developed to estimate the flexural capacity of the beamto-column joints, considering the composite effects of the slab. The comparison between the calculation, experiment, and simulation results indicates that the proposed formula can reasonably predict the flexural strength of beam-to-column joints with concrete slab.
- slab effect /
- external diaphragm /
- beam-to-column joints /
- composite structures /
- nonlinear finite element analysis

HTML全文

圖 1 有限元模型

Figure 1. Finite element model

下載: 全尺寸圖片幻燈片

圖 2 混凝土本構關系

Figure 2. Constitutive relation of concrete

下載: 全尺寸圖片幻燈片

圖 3 混凝土損傷定義

Figure 3. Cracking damage of concrete

下載: 全尺寸圖片幻燈片

圖 4 滯回曲線對比.(a) ST-W/O; (b) ST-W

Figure 4. Comparison of hysteretic curves: (a) ST-W/O; (b) ST-W

下載: 全尺寸圖片幻燈片

圖 5 骨架曲線對比.(a) ST-W/O; (b) ST-W

Figure 5. Comparison of skeleton curves: (a) ST-W/O; (b) ST-W

下載: 全尺寸圖片幻燈片

圖 6 尺寸對梁端抗彎承載力的影響

Figure 6. Effect of specimen size on the flexural capacity

下載: 全尺寸圖片幻燈片

圖 7 不同軸壓比下節點梁端彎矩-轉角曲線

Figure 7. Effect of axial-load ratio on the flexural capacity

下載: 全尺寸圖片幻燈片

圖 8 不同樓板厚度下梁端彎矩-轉角曲線

Figure 8. Effect of slab thickness on the flexural capacity

下載: 全尺寸圖片幻燈片

圖 9 不同樓板強度梁端彎矩-轉角曲線

Figure 9. Effect of slab concrete strength on flexural capacity

下載: 全尺寸圖片幻燈片

圖 10 不同方鋼管壁寬厚比梁端彎矩-轉角關系曲線

Figure 10. Effect of D/t on the flexural capacity

下載: 全尺寸圖片幻燈片

圖 11 不同寬厚比下節點域應力云圖.(a) D/t=50; (b) D/t=40; (c) D/t=33; (d) D/t=29; (e) D/t=25; (f) D/t=22

Figure 11. Effect of D/t on Von Mises stress of panel zone: (a) D/t=50; (b) D/t=40; (c) D/t=33; (d) D/t=29; (e) D/t=25; (f) D/t=22

下載: 全尺寸圖片幻燈片

圖 12 不同寬厚比下節點域等效塑性應變圖.(a) D/t=50; (b) D/t=40; (c) D/t=33; (d) D/t=29; (e) D/t=25; (f) D/t=22

Figure 12. Effect of D/t on equivalent plastic strain of panel zone: (a) D/t=50; (b) D/t=40; (c) D/t=33; (d) D/t=29; (e) D/t=25; (f) D/t=22

下載: 全尺寸圖片幻燈片

圖 13 計算簡化模型.(a) V_p≤F_{c, eff}; (b) V_p > F_{c, eff}

Figure 13. Analysis model: (a) V_p≤F_{c, eff}; (b) V_p > F_{c, eff}

下載: 全尺寸圖片幻燈片

圖 14 外環板破壞機構示意圖

Figure 14. Failure modes of external diaphragm

下載: 全尺寸圖片幻燈片

圖 15 外環板的梁柱連接節點的結構示意圖

Figure 15. Details of beam-to-column joint with external diaphragm

下載: 全尺寸圖片幻燈片

表 1 試驗和有限元的初期剛度、屈服點和塑性點對比

Table 1. Comparison of initial shear stiffness, yield moment, and plastic moment

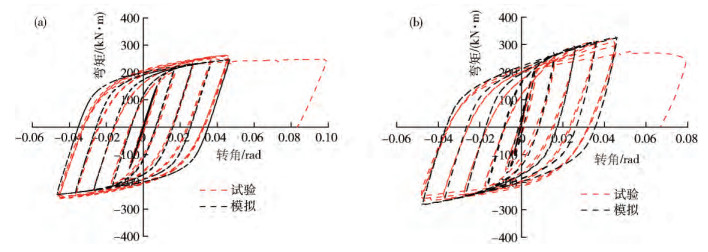
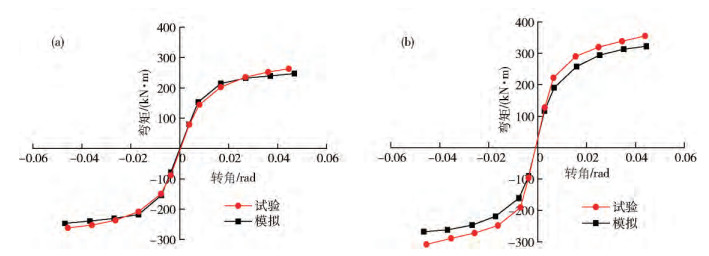
試件編號	加載方向	初始剛度/(kN·m·rad^-1)			屈服強度/(kN·m)			塑性強度/(kN·m)
試件編號	加載方向	試驗值	數值模擬	誤差/%	試驗值	數值模擬	誤差/%	試驗值	數值模擬	誤差/%
ST-W/O	正向	20498	21202	3.43	170	175	2.94	209	224	7.18
ST-W/O	負向	23653	21744	7.72	159	168	5.66	212	213	0.47
ST-W	正向	41737	43577	4.41	186	202	8.60	236	250	5.93
ST-W	負向	24717	26024	5.29	167	183	9.58	216	232	7.41

下載: 導出CSV

表 2 試件計算模型參數

Table 2. Details of parametric studies

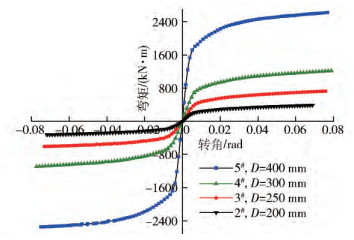
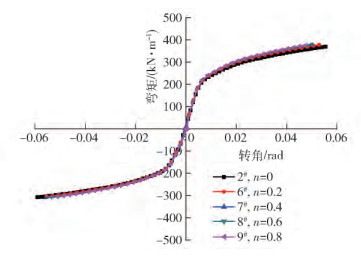
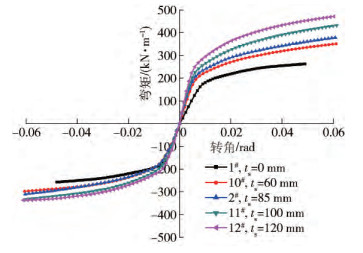
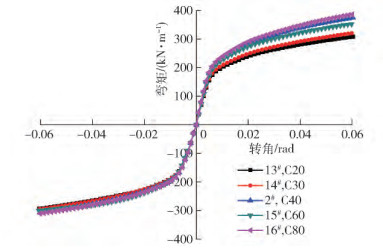
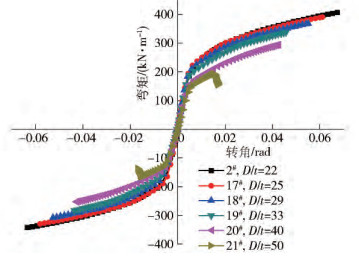
模型編號	方鋼管/(mm × mm × mm)	梁/(mm × mm × mm × mm)	方鋼管柱寬，D/mm	軸壓比，n	樓板厚度，t_s/mm	樓板強度等級	柱寬/厚比，D/t
1^#(ST-W/O)	200×200×9	300×120×6×12	200	0	0	C40	22
2^#(ST-W)	200×200×9	300×120×6×12	200	0	85	C40	22
3^#	250×250×9	375×150×7.5×15	250	0	85	C40	22
4^#	300×300×13.5	450×180×9×18	300	0	85	C40	22
5^#	400×400×18	600×240×12×24	400	0	85	C40	22
6^#	200×200×9	300×120×6×12	200	0.2	85	C40	22
7^#	200×200×9	300×120×6×12	200	0.4	85	C40	22
8^#	200×200×9	300×120×6×12	200	0.6	85	C40	22
9^#	200×200×9	300×120×6×12	200	0.8	85	C40	22
10^#	200×200×9	300×120×6×12	200	0	60	C40	22
11^#	200×200×9	300×120×6×12	200	0	100	C40	22
12^#	200×200×9	300×120×6×12	200	0	120	C40	22
13^#	200×200×9	300×120×6×12	200	0	85	C20	22
14^#	200×200×9	300×120×6×12	200	0	85	C30	22
15^#	200×200×9	300×120×6×12	200	0	85	C60	22
16^#	200×200×9	300×120×6×12	200	0	85	C80	22
17^#	200×200×8	300×120×6×12	200	0	85	C40	25
18^#	200×200×7	300×120×6×12	200	0	85	C40	29
19^#	200×200×6	300×120×6×12	200	0	85	C40	33
20^#	200×200×5	300×120×6×12	200	0	85	C40	40
21^#	200×200×4	300×120×6×12	200	0	85	C40	50

下載: 導出CSV

表 3 不同尺寸試件在性能點的梁端抗彎承載力

Table 3. Effect of specimen size on the moment-rotation behavior

試件編號	柱寬，D/mm	加載方向	K₀^FEM/(kN·rad^-1)	θ_y^FEM/rad	M_y^FEM/(kN·m)	θ_p^FEM/rad	M_p^FEM/(kN·m)
5^#	400	正向	336867	0.0049	1621	0.0090	1859
5^#	400	負向	197502	0.0060	1456	0.0095	-1732
4^#	300	正向	141683	0.0055	671	0.0093	754
4^#	300	負向	87631	-0.0088	-609	0.0142	-675
3^#	250	正向	82665	0.0064	387	0.0102	464
3^#	250	負向	49367	-0.0090	-355	-0.0151	-393
2^#	200	正向	43577	0.0056	202	0.0097	250
2^#	200	負向	26024	-0.0090	-183	-0.0157	-216

下載: 導出CSV

表 4 不同尺寸下的單位截面抗彎系數梁端抗彎承載力的比值

Table 4. Effect of specimen size on M₂₃, M₂₄and M₂₅

單位截面抗彎系數梁端抗彎承載力比值	正向荷載		負向荷載
單位截面抗彎系數梁端抗彎承載力比值	屈服點	塑性點	屈服點	塑性點
M₂₃	0.98	0.95	0.99	0.93
M₂₄	0.98	0.89	0.99	0.93
M₂₅	1.00	0.93	0.99	1.00

下載: 導出CSV

表 5 樓板強度等級

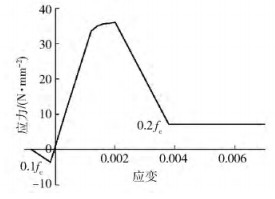
Table 5. Slab concrete strength

強度等級	立方體抗壓強度標準值，f_{cu, k}/MPa	抗壓強度，f_c/MPa
C20	20	9.6
C30	30	14.3
C40	40	21.1
C60	60	23.1
C80	80	35.9

下載: 導出CSV

表 6 塑性點彎矩計算值與試驗值/有限元值對比

Table 6. Comparison of calculation results with experiment or FEM results

參數名稱	參數值	正向加載			負向加載
參數名稱	參數值	M_p^CAL/(kN·m)	M_p^EXP或M_p^FEM/(kN·m)	M_p^CAL/M_p^EXP或M_p^CAL/M_p^FEM	M_p^CAL/(kN·m)	M_p^EXP或M_p^FEM/(kN·m)	M_p^CAL/M_p^EXP或M_p^CAL/M_p^FEM
ST-W/O^*	—	198.1	209.0	0.95	198.1	212.0	0.93
ST-W^**	—	231.5	236.0	0.98	198.1	216.0	0.92
樓板厚度，t_s/mm	60	216.9	224.5	0.97	198.1	186.6	1.06
	85	231.4	236.0	0.98	198.1	216.0	0.92
	100	236.6	266.0	0.89	198.1	199.8	0.99
	120	243.4	287.0	0.85	198.1	203.2	0.97
樓板混凝土強度等級	C20	215.2	204.1	1.05	198.1	196.9	1.01
	C30	223.8	220.0	1.02	198.1	196.6	1.01
	C40	231.5	236.0	0.98	198.1	216.0	0.92
	C60	231.5	264.5	0.87	198.1	199.0	1.00
	C80	231.5	270.4	0.86	198.1	198.4	1.00
柱寬厚比，D/t	22	231.5	236.0	0.98	198.1	216.0	0.92
	25	219.6	231.7	0.95	188	198.1	0.95
	29	208.8	215.7	0.97	178.7	183.4	0.97
	33	199.2	204.0	0.98	170.5	173.1	0.98
	40	190.8	176.9	1.08	163.3	152.2	1.07
	50	183.7	164.7	1.12	157.3	141.5	1.11
??注: ^和^*為實驗.

下載: 導出CSV

259luxu-164

參考文獻(16)

[1]	Miller D K. Lessons learned from the Northridge earthquake. Eng Struct, 1998, 20(4-6): 249 doi: 10.1016/S0141-0296(97)00031-X
[2]	Youssef N F G, Bonowitz D, Gross J L. A Survey of Steel Moment-Resisting Frame Buildings Affected by the 1994 Northridge Earthquake. Rep. No NISTIR-5625. Gaithersburg (Md): US National Institute of Standards and Technology, 1995
[3]	Nakashima M, lnoue K, Tada M. Classification of damage to steel buildings observed in the 1995 Hyogoken-Nanbu earthquake. Eng Struct, 1998, 20(4-6): 271 doi: 10.1016/S0141-0296(97)00019-9
[4]	Nie J G, Huang Y, Fan J S. Experimental study on load-bearing behavior of rectangular CFST frame considering composite action of floor slab. J Build Struct, 2011, 32(3): 99 https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201103016.htm 聶建國, 黃遠, 樊健生. 考慮樓板組合作用的方鋼管混凝土組合框架受力性能試驗研究. 建筑結構學報, 2011, 32(3): 99 https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201103016.htm
[5]	Tao M X, Nie J G. Design methods of composite frame systems considering the slab spatial composite effect-Part Ⅰ: ultimate loading capacity. China Civil Eng J, 2012, 45(11): 39 https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201211006.htm 陶慕軒, 聶建國. 考慮樓板空間組合作用的組合框架體系設計方法(Ⅰ) -極限承載能力. 土木工程學報, 2012, 45(11): 39 https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201211006.htm
[6]	Tao M X, Nie J G. Design guidelines of composite frame systems considering the slab spatial composite effect-Part Ⅱ: stiffness and verifications. China Civil Eng J, 2013, 46(2): 42 https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201302005.htm 陶慕軒, 聶建國. 考慮樓板空間組合作用的組合框架體系設計方法(Ⅱ) -剛度及驗證. 土木工程學報, 2013, 46(2): 42 https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201302005.htm
[7]	Cheng C T, Chan C F, Chung L L. Seismic behavior of steel beams and CFT column moment-resisting connections with floor slabs. J Constr Steel Res, 2007, 63(11): 1479 doi: 10.1016/j.jcsr.2007.01.014
[8]	Qian W W, Li W, Han L H, et al. Analytical behavior of concrete-encased concrete-filled steel tubular column to steel beam joints with RC slabs. Eng Mech, 2016, 33(Suppl): 95 https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2016S1018.htm 錢煒武, 李威, 韓林海, 等. 帶樓板鋼管混凝土疊合柱-鋼梁節點抗震性能數值分析. 工程力學, 2016, 33(增刊): 95 https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2016S1018.htm
[9]	Liao F Y, Han L H, Tao Z. Behaviour of composite joints with concrete encased CFST columns under cyclic loading: Experiments. Eng Struct, 2014, 59: 745 doi: 10.1016/j.engstruct.2013.11.030
[10]	Chen Y Y, Shen Z Y, Zhan C, et al. Three lines limit-analysis model for CHS K-Joints and its verification by tests. China Clivil Eng J, 1999, 32(6): 26 doi: 10.3321/j.issn:1000-131X.1999.06.004 陳以一, 沈祖炎, 詹琛, 等. 直接匯交節點三重屈服線模型及試驗驗證. 土木工程學報, 1999, 32(6): 26 doi: 10.3321/j.issn:1000-131X.1999.06.004
[11]	Tateyama E, Inoue K, Sugimoto S, et al. Study on ultimate bending strength and deformation capacity of H-shaped beam connected to RHS column with through diaphragms. J Struct Constr Eng, 1988, 389: 109 立山英二, 井上一朗, 杉本正三. 通しダイヤフラム形式で角形鋼管柱に接合されるH形斷面はりの耐力と変形性能に関する研究. 日本建築學會構造系論文報告集. 1988, 389: 109
[12]	Mansfield E H. Studies in collapse analysis of rigid-plastic plates with a square yield diagram//Proceeding of the Royal Society London. London, 1957: 311
[13]	Mou B, Wang L L, Zhang C W, et al. Aseismic performance of beam-to-column joints with external-diaphragm considering the slab effect: experimental investigation. Eng Mech, 2018, 35(2): 160 https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201802020.htm 牟犇, 王玲玲, 張春巍, 等. 考慮樓板影響的外環板式梁柱節點抗震性能: 試驗研究. 工程力學, 2018, 35(2): 160 https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201802020.htm
[14]	Jiang J J, Lu X Z, Ye L P. Finite Element Analysis of Concrete Structures. Beijing: Tsinghua University Press, 2005 江見鯨, 陸新征, 葉列平. 混凝土結構有限元分析. 北京: 清華大學出版社, 2005
[15]	Ministry of Housing and Urban-Rural Construction of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB50010-2010 Code for Design of Concrete Structures. Beijing: Standards Press of China, 2010 中華人民共和國住房和城鄉建設部, 中華人民共和國國家質量監督檢驗檢疫總局. GB50010-2010混凝土結構設計規范. 北京: 中國標準出版社, 2010
[16]	Mou B. Strength and Collapse Behavior of Offset Beam-to-Column Connection Panels with Exterior Diaphragms in Steel Structure and Concrete Filled Steel Tubular Structure[Dissertation]. Fukuoka: Kyushu University, 2015