連鑄流動與凝固耦合模擬中糊狀區系數的表征及影響

李少翔; 張曉萌; 李亮; 蘭鵬; 唐海燕; 張家泉

doi:10.13374/j.issn2095-9389.2019.02.006

連鑄流動與凝固耦合模擬中糊狀區系數的表征及影響

doi: 10.13374/j.issn2095-9389.2019.02.006

北京科技大學冶金與生態工程學院, 北京 100083

基金項目:

國家自然科學基金資助項目 U1860111

國家自然科學基金資助項目 51604021

北京市自然科學基金資助項目 2174077

北京科技大學本科教育教學改革資助項目 JG2017M11

詳細信息

通訊作者:
張家泉, E-mail: jqzhang@metall.ustb.edu.cn

中圖分類號: TF777.2
計量
- 文章訪問數: 2116
- HTML全文瀏覽量: 726
- PDF下載量: 85
- 被引次數: 0
出版歷程
- 收稿日期: 2018-03-01
- 刊出日期: 2019-02-01

Representation and effect of mushy zone coefficient on coupled flow and solidification simulation during continuous casting

School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China

More Information

Corresponding author: ZHANG Jia-quan, E-mail: jqzhang@metall.ustb.edu.cn

摘要

摘要: 分析提出了連鑄流動與凝固耦合數值模擬中, 鋼液在兩相區流動時的糊狀區系數(A_mush)與滲透率的關系; 通過建立大方坯連鑄結晶器三維耦合數值模型, 揭示了不同糊狀區系數對鋼液流動、傳熱與凝固進程的影響, 以及早期相關研究結果差異的源頭.結果表明: 糊狀區系數越大, 鋼液在糊狀區內的流動阻力越強, 凝固時鋼液流動速度降低越快.采用較大的糊狀區系數時, 糊狀區呈較窄的"帶狀"分布在固液相之間; 當糊狀區系數較小時, 糊狀區范圍變大, 鋼液在結晶器內溫降過快, 自由液面處出現過冷現象, 凝固坯殼局部發生重熔.結合實驗數據驗證與模型分析, 認為糊狀區系數取值1×10⁸~5×10⁸ kg·m^-3·s^-1可以較可靠地揭示連鑄結晶器內的實際凝固現象.
- 連鑄 /
- 數值模擬 /
- 流動 /
- 凝固 /
- 糊狀區系數
Abstract: The mushy zone refers to the region of the solid-liquid system where the temperature is between the liquidus and solidus temperatures. In this zone, the turbulence of the interdendritic flow is reduced by blockage of dendrites. The mushy zone coefficient (A_mush) is an important calculating parameter in the continuous casting numerical simulation process, which strongly affects the prediction of fluid flow and solidification behavior in the mold zone. However, most researchers have neglected the influence of the mushy zone coefficient, and the correct expression of this coefficient is rarely found in the literature. Generally, the lower default value of 1×10⁵ kg·m^-3·s^-1 is used in the model, which leads to unrealistic results. In this study, the relationship between the mushy zone coefficient and permeability was analyzed, and the expression of the mushy zone coefficient was proposed. A coupled flow and solidification numerical model was developed to evaluate the effect of the mushy zone coefficient on the melt flow and solidification phenomena in a bloom continuous casting mold. Results show that the higher the value of the mushy zone coefficient, the stronger the damping becomes, and the faster the velocity drops as melt solidifies. A relatively high value of the mushy zone coefficient generates a "banded" form of mushy zone sandwiched between the solid and liquid phases in the mold zone. When the mushy zone coefficient is at a lower value, a wider mushy zone is obtained and the melt cools down rapidly in the mold region. In addition, the temperature at free surface is relatively low with supercooling, and the solidified shell remelts locally. The model is validated through comparison with measurements of shell thickness on a breakout shell. The value of the mushy zone coefficient ranging from 1×10⁸ to 5×10⁸ kg·m^-3·s^-1 is suggested.
- continuous casting /
- numerical simulation /
- fluid flow /
- solidification /
- mushy zone coefficient

HTML全文

圖 1 二次枝晶間距測量值

Figure 1. SDAS against distance from outer surface of breakout shell

下載: 全尺寸圖片幻燈片

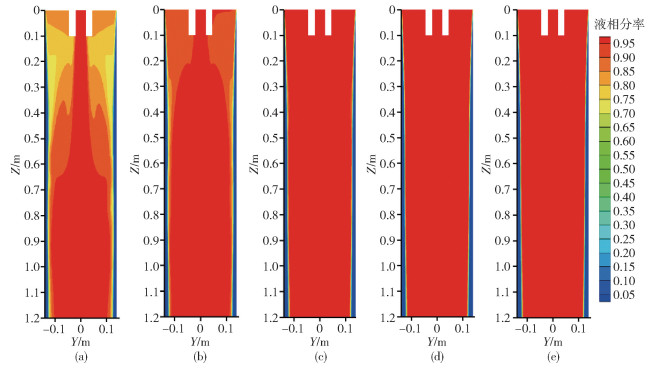
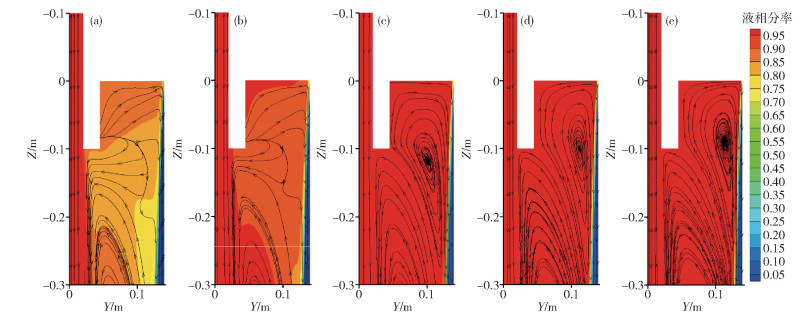
圖 2 不同糊狀區系數下結晶器寬面中心對稱面上的液相分率分布. (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

Figure 2. Distributions of liquid fraction on central symmetry plane of strand under different cases: (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

下載: 全尺寸圖片幻燈片

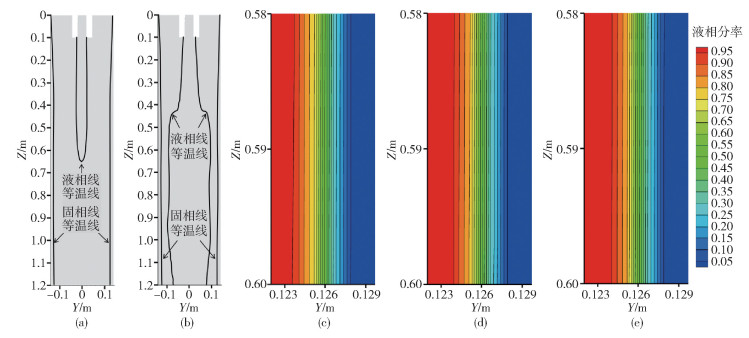
圖 3 不同糊狀區系數下結晶器寬面中心對稱面上的糊狀區示意圖. (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

Figure 3. Diagrams of mushy zone on central symmetry plane of strand under different cases: (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

下載: 全尺寸圖片幻燈片

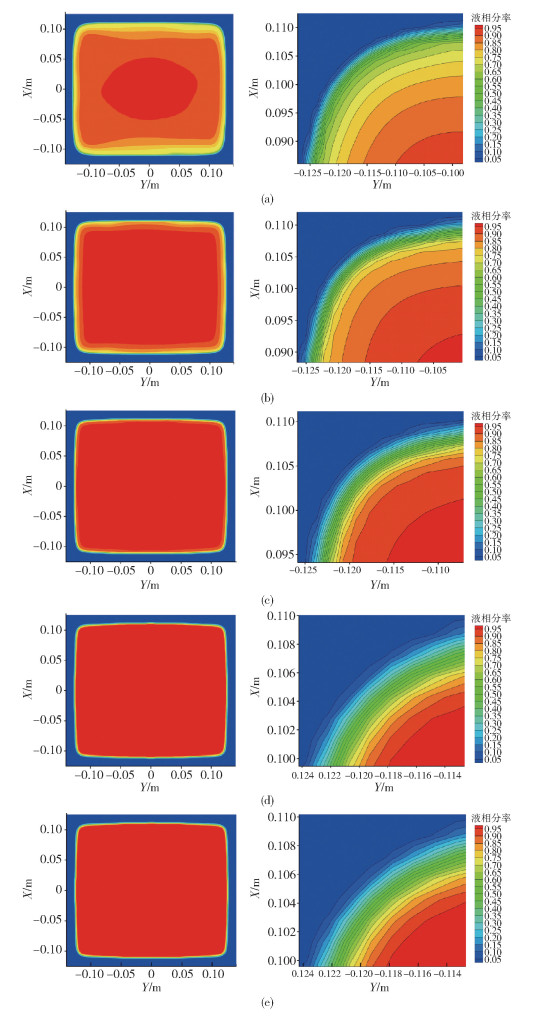
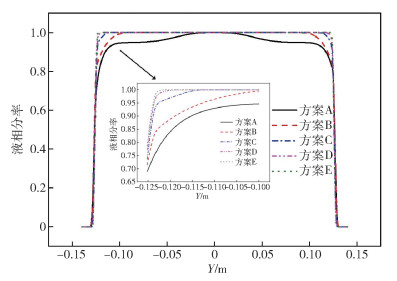
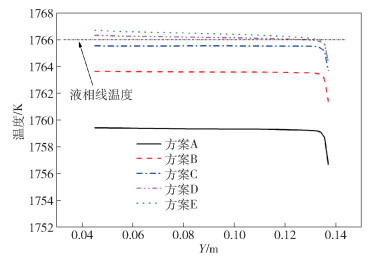
圖 4 不同糊狀區系數下結晶器出口處鑄坯橫截面上的液相分率分布云圖. (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

Figure 4. Liquid fraction contour on cross plane at mold exit under different cases: (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

下載: 全尺寸圖片幻燈片

圖 5 不同糊狀區系數下結晶器出口處液相分率沿鑄坯寬度方向的變化曲線

Figure 5. Variation of liquid fraction along Y direction at mold exit

下載: 全尺寸圖片幻燈片

圖 6 不同糊狀系區數下結晶器中心線上的鋼液溫度沿拉坯方向的分布

Figure 6. Temperature variations at strand center along casting direction

下載: 全尺寸圖片幻燈片

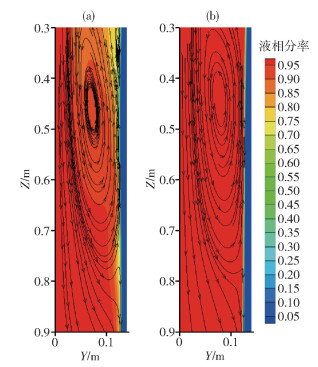
圖 7 不同糊狀區系數下彎月面處的鋼液流線圖與液相分率云圖. (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

Figure 7. Liquid fraction contour and streamline around meniscus: (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 1×10⁶ kg ·m^-3 ·s^-1; (c) 1×10⁷ kg ·m^-3 ·s^-1; (d) 1×10⁸ kg ·m^-3 ·s^-1; (e) 5×10⁸ kg ·m^-3 ·s^-1

下載: 全尺寸圖片幻燈片

圖 8 不同糊狀區系數下自由液面處的鋼液溫度沿寬面方向的分布

Figure 8. Variation of temperature along Y direction at free surface

下載: 全尺寸圖片幻燈片

圖 9 不同糊狀區系數下寬面中心線上的坯殼厚度沿拉坯方向的變化情況

Figure 9. Shell thickness at center line of wide face along casting direction

下載: 全尺寸圖片幻燈片

圖 10 不同糊狀區系數時鋼液流線圖與液相分率云圖. (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 5×10⁸ kg ·m^-3 ·s^-1

Figure 10. Liquid fraction contour and streamline under different cases: (a) 1×10⁵ kg ·m^-3 ·s^-1; (b) 5×10⁸ kg ·m^-3 ·s^-1

下載: 全尺寸圖片幻燈片

圖 11 漏鋼凝固坯殼示意圖

Figure 11. Schematic of shell from breakout

下載: 全尺寸圖片幻燈片

圖 12 坯殼厚度數值計算值與測量值及經驗公式計算值對比

Figure 12. Comparison of shell thickness under different conditions

下載: 全尺寸圖片幻燈片

表 1 數值模擬方案

Table 1. Cases calculated for this study

方案	糊狀區系數/(kg·m^-3·s^-1)
A	1×10⁵
B	1×10⁶
C	1×10⁷
D	1×10⁸
E	5×10⁸

下載: 導出CSV

表 2 鋼液熱物性參數及模擬參數列表

Table 2. Thermophysical properties and simulation conditions in this study

參數名稱	數值
結晶器工作長度/mm	645
鑄坯斷面/mm²	250×280
拉速/(m·min^-1)	1.05
水口插入深度/mm	100
水口內徑/mm	40
水口外徑/mm	90
鋼液比熱容/(J·kg^-1·K^-1)	680
鋼液導熱系數/(W·m^-1·K^-1)	29
鋼液黏度/(kg·m^-1·s^-1)	0.006
鋼液密度/(kg·m^-3)	7020
固相線溫度/K	1718
液相線溫度/K	1766
凝固潛熱/(J·kg^-1)	270000
熱膨脹系數/K^-1	1×10^-4
過熱度/K	30

下載: 導出CSV

259luxu-164

參考文獻(27)

[1]	Thomas B G, Mika L J, Najjar F M. Simulation of fluid flow inside a continuous slab-casting machine. Metall Trans B, 1990, 21(2): 387 doi: 10.1007/BF02664206
[2]	Thomas B G, Zhang L F. Mathematical modeling of fluid flow in continuous casting. ISIJ Int, 2001, 41(10): 1181 doi: 10.2355/isijinternational.41.1181
[3]	Fujisaki K. Magnetohydrodynamic solidification calculation in Darcy flow[steel casting]. IEEE Trans Magn, 2003, 39(6): 3541 doi: 10.1109/TMAG.2003.819456
[4]	Chakraborty S, Dutta P. Effects of dendritic arm coarsening on macroscopic modelling of solidification of binary alloys. Mater Sci Technol, 2001, 17(12): 1531 doi: 10.1179/026708301101509782
[5]	Pfeiler C, Thomas B G, Wu M, et al. Solidification and particle entrapment during continuous casting of steel. Steel Res Int, 2008, 79(8): 599 doi: 10.1002/srin.200806172
[6]	Gu J P, Beckermann C. Simulation of convection and macrosegregation in a large steel ingot. Metall Mater Trans A, 1999, 30(5): 1357 doi: 10.1007/s11661-999-0284-5
[7]	Yang H L, Zhang X Z, Deng K W, et al. Mathematical simulation on coupled flow, heat, and solute transport in slab continuous casting process. Metall Mater Trans B, 1998, 29(6): 1345 doi: 10.1007/s11663-998-0058-2
[8]	Aboutalebi M R, Hasan M, Guthrie R I L. Coupled turbulent flow, heat, and solute transport in continuous casting processes. Metall Mater Trans B, 1995, 26(4): 731 doi: 10.1007/BF02651719
[9]	Seyedein S H, Hasan M. A three-dimensional simulation of coupled turbulent flow and macroscopic solidification heat transfer for continuous slab casters. Int J Heat Mass Transfer, 1997, 40(18): 4405 doi: 10.1016/S0017-9310(97)00064-1
[10]	Aboutalebi M R, Guthrie R I L, Seyedein S H. Mathematical modeling of coupled turbulent flotw and solidification in a single belt caster with electromagnetic brake. Appl Math Modell, 2007, 31(8): 1671 doi: 10.1016/j.apm.2006.05.012
[11]	Netto P G Q, Guthrie R I L. Modelling of a novel configuration for single-belt caster: the influence of empirical parameters on the solidification profile. ISIJ Int, 2000, 40(5): 460 doi: 10.2355/isijinternational.40.460
[12]	Sun H B, Zhang J Q. Study on the macrosegregation behavior for the bloom continuous casting: model development and validation. Metall Mater Trans B, 2014, 45(3): 1133 doi: 10.1007/s11663-013-9986-6
[13]	Sun H B, Zhang J Q. Effect of feeding modes of molten steel on the mould metallurgical behavior for round bloom casting. ISIJ Int, 2011, 51(10): 1657 doi: 10.2355/isijinternational.51.1657
[14]	He M L, Wang N, Chen M, et al. Physical and numerical simulation of the fluid flow and temperature distribution in bloom continuous casting mold. Steel Res Int, 2017, 88(9): 1600447 doi: 10.1002/srin.201600447
[15]	Trindade L B, Nadalon J E A, Contini A C, et al. Modeling of solidification in continuous casting round billet with mold electromagnetic stirring (M-EMS). Steel Res Int, 2017, 88(4): 1600319 doi: 10.1002/srin.201600319
[16]	Hietanen P T, Louhenkilpi S, Yu S. Investigation of solidification, heat transfer and fluid flow in continuous casting of steel using an advanced modeling approach. Steel Res Int, 2017, 88(7): 1600355 doi: 10.1002/srin.201600355
[17]	Wang Q Q. Stundy on the Multiphase Flow, Heat Transfer and Solidification, Motion and Entrapment of Inclusions during Continuous Casting [Dissertation]. Beijing: University of Science and Technology Beijing, 2016 王強強. 連鑄過程多相流、傳熱凝固及夾雜物運動捕獲的研究[學位論文]. 北京: 北京科技大學, 2016
[18]	Voller V R, Prakash C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int J Heat Mass Transfer, 1987, 30(8): 1709 doi: 10.1016/0017-9310(87)90317-6
[19]	Carman P C. Fluid flow through granular beds. Trans Inst Chem Eng, 1937, 15: 150 http://ci.nii.ac.jp/naid/10003392892
[20]	Minakawa S, Samarasekera I V, Weinberg F. Centerline porosity in plate castings. Metall Trans B, 1985, 16(4): 823 doi: 10.1007/BF02667519
[21]	Won Y M, Thomas B G. Simple model of microsegregation during solidification of steels. Metall Mater Trans A, 2001, 32(7): 1755 doi: 10.1007/s11661-001-0152-4
[22]	Jiang D B, Zhu M Y. Flow and solidification in billet continuous casting machine with dual electromagnetic stirrings of mold and the final solidification. Steel Res Int, 2015, 86(9): 993 doi: 10.1002/srin.201400281
[23]	Ji Y, Tang H Y, Lan P, et al. Effect of dendritic morphology and central segregation of billet castings on the microstructure and mechanical property of hot-rolled wire rods. Steel Res Int, 2017, 88(8): 1600426 doi: 10.1002/srin.201600426
[24]	Jones W P, Launder B E. The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence. Int J Heat Mass Transfer, 1973, 16(6): 1119 doi: 10.1016/0017-9310(73)90125-7
[25]	Lai K Y M, Salcudean M, Tanaka S, et al. Mathematical modeling of flows in large tundish systems in steelmaking. Metall Trans B, 1986, 17(3): 449 doi: 10.1007/BF02670209
[26]	Savage J, Pritchard W H. The problem of rupture of the billet in the continuous casting of steel. J Iron Steel Inst, 1954, 178(3): 269 http://www.researchgate.net/publication/284154760_The_problem_of_rupture_of_the_billet_in_the_continuous_casting_of_steel
[27]	Cai K K. Continuous Casting Mold. Beijing: Metallurgical Industry Press, 2008 蔡開科. 連鑄結晶器. 北京: 冶金工業出版社, 2008